Задачи с коаксиальным кабелем

Разделы

Дополнительно

Задача по физике — 10976

Коаксиальный кабель состоит из двух концентрических проводящих цилиндров. Один конец ($x=0$) кабеля подсоединен к генератору переменного напряжения $V(t) = V_ <0>\cos \omega t$. Другой конец ($x = l$) закрыт проводящей пластиной. Индуктивность и емкость единицы длины кабеля равны $L_<0>$ и $C_<0>$. Поле в таком кабеле можно представить в виде суперпозиции двух волн: падающей и отраженной от закороченного конца. Амплитуды и фазы этих волн должны быть подобраны так, чтобы суммарное напряжение между проводниками было равно нулю при $x=l$ и $V_ <0>\cos \omega t$ при $x=0$.
а) Напишите выражения для падающей и отраженной волн.
б) Нарисуйте кривую зависимости напряжения между проводниками от расстояния $x$, если длина кабеля $l$ равна $5 \pi c/2 \omega$ ($x$ — скорость света). Укажите значения $x$, для которых напряжение максимально.
в) Чему равен ток в точках $x=0, x = \frac <2>= \frac<1> <2>\frac<5 \pi c><2 \omega>$ и $x = l = \frac<5 \pi c><2 \omega>$?
г) Предполагая источник напряжения идеальным, определите средний момент сил, который должен быть приложен к его ротору, чтобы последний вращался с угловой скоростью $\omega$.

Задача по физике — 10977

Линия передачи с характеристическим импедансом $Z_<1>$ соединена с другой линией с; характеристическим импедансом $Z_<2>$.
Покажите, что если система работает от генератора, подключенного к первой линии ($Z_<1>$), «коэффициент отражения», определяемый отношением $\frac > >$, равен

а «коэффициент пропускания»

Задача по физике — 10978

Выразите в мегатоннах (мгт) энергию магнитного поля Земли, заключенную во всем пространстве, внешнем по отношению к Земле (1 мгт — энергия, освобождаемая при взрыве 1 млн. тонн тринитротолуола, т. е. $4,2 \cdot 10^ <15>дж$). Предположите, что магнитное поле Земли — это поле диполя с напряженностью на экваторе примерно около $2/3 гс$ ($2/3 \cdot 10^ <-4>вебер/м^<2>$).
Как вы считаете, может ли водородная бомба 1 мгт, взорванная высоко над поверхностью Земли, существенно исказить магнитное поле Земли?

Задача по физике — 10979

Вычислите поток вектора Пойнтинга $\vec$ через поверхность длинного прямолинейного провода, сопротивление единицы длины которого равно $R$. Сравните ваш результат с омическими потерями.

Задача по физике — 10980

Длинный коаксиальный кабель изготовлен из двух идеально проводящих концентрических цилиндров. Один конец кабеля подсоединен, к электрической батарее, напряжение на клеммах которой равно $V$. К другому концу кабеля присоединено сопротивление $R$. Следовательно, ток, протекающий по кабелю, равен $I=V/R$. С помощью вектора Пойн-тинга вычислите скорость потока энергии.

Задача по физике — 10981

Задача по физике — 10982

Плоская электромагнитная волна, падая на свободный электрон, заставляет его осциллировать. Найдите отношение энергии, излучаемой электроном в единицу времени, к плотности потока энергии падающей электромагнитной волны. Частота волны предполагается малой. Поэтому влиянием магнитного поля $\vec$ волны на движение электрона можно пренебречь.

Задача по физике — 10983

Частица пыли в Солнечной системе испытывает действие двух сил: силы притяжения к Солнцу и планетам и силы светового давления, пропорциональной ее поперечному сечению. Существует такой размер частицы, при котором эти силы уравновешивают друг друга. Предполагая, что частица имеет форму шарика и поглощает весь падающий на нее свет, найдите радиус частицы, отвечающий ее равновесию в поле этих двух сил. Объяснение того факта, что «хвосты» комет направлены в сторону от Солнца, покоится на предположении о существовании такого равновесия и о том, что «хвост» кометы состоит из частиц малого размера, возможно даже из молекул газа. Разумно ли такое объяснение? Мощность, излучаемая Солнцем, равна $4 \cdot 10^ <26>вт$, его масса $2 \cdot 10^ <30>кг$.

Задача по физике — 10984

На полый тороид, средний радиус которого равен $R$, а радиус поперечного сечения $r (r \ll R)$, намотано $N$ витков проволоки. В момент времени $t = 0$ по проволоке пропускается ток, сила которого нарастает со временем по линейному закону

а) Найдите магнитное поле и энергию, запасенную в тороиде к моменту времени $t$.
б) Найдите направление и величину вектора Пойн-тинга в любой внутренней точке тороида в момент времени $t$.
в) Используя вектор Пойнтинга, найдите скорость изменения со временем энергии электромагнитного поля внутри тороида в произвольный момент времени. Убедитесь в правильности вашего ответа, используя решение к пункту (а) задачи.

Задача по физике — 10985

В момент времени $t=0$ частица массы $m$ с зарядом $q$ покоится в начале координат. На частицу действует однородное электрическое поле $\vec$, направленное по оси $y$, и однородное магнитное поле $\vec$, направленное по оси $z$.
а) Найдите последующее движение частицы, т. е. ее координаты $x(t), y(t), z(t)$, предполагая движение нерелятивистским. Какое условие на $\vec$ и $\vec$ накладывает это предположение?
б) Какой характер будет иметь движение в том случае, если $E/B > c$?
в) Пусть разность потенциалов между двумя параллельными пластинами, одна из которых совпадает с плоскостью $xz (y =0)$, а другая находится на расстоянии $d (y=d)$, равна $V_ <0>= E \cdot d$, и между пластинами приложено магнитное поле, параллельное пластинам. Пусть кинетическая энергия электронов, вылетающих из отрицательно заряженной пластины, равна нулю. При каком значении’ напряженности магнитного поля испущенные электроны не будут достигать другой пластины?

Задача по физике — 10987

На частоте примерно 6 Мгц ионосфера становится прозрачной. В рамках модели свободных электронов оцените плотность электронов в ионосфере.

Задача по физике — 10988

К металлу в течение долгого времени приложено постоянное электрическое поле, а затем оно мгновенно выключается. Используя модель свободных электронов, покажите, что время релаксации (т. е. время, в течение которого дрейфовая скорость электронов падает в $e$ раз) равно $\tau$, где $\tau$ — среднее время между столкновениями.

Задача по физике — 10989

В циклотроне, рассчитанном на низкие энергии, период обращения протонов по круговой орбите составляет 0,13 мксек. Ядерный магнитный резонанс для протона в магнитном поле циклотрона наступает при частоте 21 Мгц. Определите по этим данным $g$-фактор протона.

Задача по физике — 10990

В $1 см^<3>$ парамагнитной соли содержится $10^<22>$ атомов с магнитным моментом в один магнетон Бора каждый.
Соль помещается в однородное магнитное поле напряженностью $10 000 гс (1 вебер/м^<2>)$. Выразите в процентах избыток параллельных полю спинов при комнатной температуре и температуре жидкого гелия.

Задача по физике — 10991

Шар радиуса $a$ однородно намагничен так, что его полный магнитный момент равен $4/3 \pi a^<3>M$, где $M$ — намагниченность. Каковы должны быть поверхностные токи, создающие магнитное поле вне шара (тех же размеров), которое совпадает с полем, создаваемым намагниченным шаром. Покажите, что найденное распределение токов обладает таким же полным магнитным моментом.

Источник

2.4. Примеры решения задач

Задача № 1. Коаксиальный кабель имеет размеры d= 4 мм, D=12 мм. Заполняющей средой является диэлектрик с параметрами  = 2,4 и =1. Найти амплитуду напряжения в бегущей волне, если известно, что амплитуда тока составляет 0,4 А.

Решение: По формуле (2.1) находим

. Тогда .

Коаксиальный кабель имеет политэтиленовую изоляцию ( = 2,25) и следующие размеры в поперечном сечении: D =3 мм, d =0,9 мм. Найти погонное затухание Т-волны в данном кабеле при частоте сигнала f = 750 МГц, считая, что =5,710 7 См/м.

Решение: Погонное затухание а коаксиальном фидере определяется

(2.41)

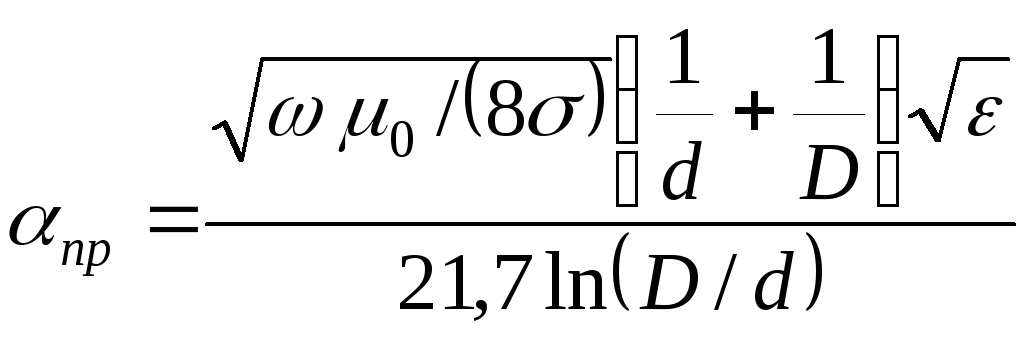
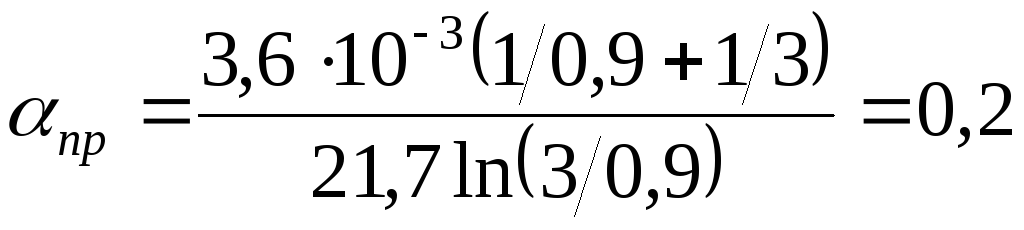
Здесь значение параметра Ом. Тогда в соответствии с формулой (2.41)

дБ/м.

Найти отношение между внешним и внутренним диаметрами коаксиальной линии передачи с волной типа Т, при котором будет минимальное затухание. Считать, что потери в диэлектрике малы. Внутренний и внешний цилиндры выполнены из одного материала.

Так как по условию задачи потери в диэлектрике малы, можем положить что  _д=0, тогда  = _м. Коэффициент ослабления _м в коаксиальной линии передачи определяем согласно формуле

П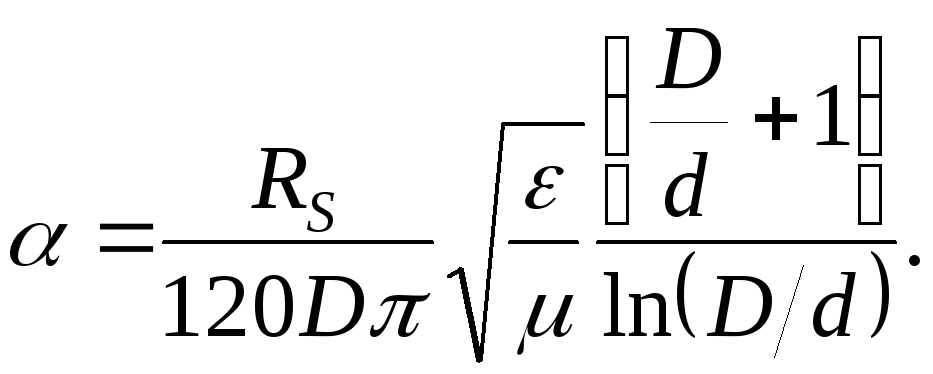реобразуем последнее выражение так, чтобы в него входило в явном виде отношениеD/d:

Для нахождения экстремума следует решить уравнение.

Полученное уравнение является трансцендентным.

Из графических построений (рис.2.5) имеем корень х = 3,6, откуда D/d == 3,6. Таким образом, минимальное затухание волны типа Т в коаксиальной линии передачи получается при отношении D/d = 3,6.

Центрирование внутреннего цилиндра воздушного коаксиального волновода осуществляют c помощью диэлектрических шайб рис.(2.6). Рассчитать диаметр D внешнего цилиндра и глубину выточек h в нем, исходя из условия отсутствия отражений. Волновое сопротивление линии Z_В=70 Ом, диаметр внутреннего цилиндра линии d = 4,5 мм, диаметр отверстия в шайбе d_ш=3,0 мм, относительная диэлектрическая проницаемость материала шайбы =2,3. Потерями в линии пренебречь.

Решение. Воздушную коаксиальную линию передачи c шайбами можно рассматривать как каскадное cоединение отрезков регулярных линий. Поскольку в плоскости стыка шайбы и воздушной линии напряжение U является непрерывной функцией координаты z, мощность может быть целиком передана из одной линии в другую без отражения, если Z_В₁= Z_В₂ , где Z_В₂— волновое сопротивление той части, где расположена шайба.

С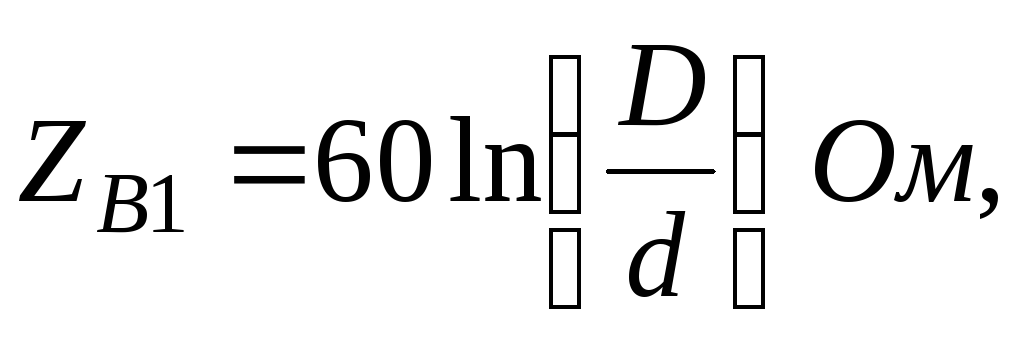огласно выражению

запишем

откуда D = 14,45 мм. Далее находим

Приравнивая и , получаем уравнение

корень которого h = 1,58 мм.

Полученное решение является приближенным, поскольку не учитываются локальные возмущения поля из-за скачков диаметров проводников.

Рассчитать волновое сопротивление, погонные емкость и индуктивность, а также предельную передаваемую мощность в несимметричной полосковой линии передачи с воздушным заполнением. Параметры линии: ширина проводника b = 5 мм, расстояние между проводником и заземленной пластиной d = 1 мм, толщина проводника t = 0,025 мм, предельно допустимое значение напряженности электрического поля в воздухе.

Решение. Так как в нашем случае b/d > 2, то волновое сопротивление несимметричной полосковой линии передачи будет определяется выражением (2.22).

Полосковая линия передачи заполнена воздухом, для которого =1, =1. Тогда

Волновое сопротивление можно определить и по более упрощенной формуле, так как в рассматриваемом случае t/d = 0,025 9 Гц. .

Решение. Общие потери определяются суммой потерь в металле и диэлектрике  = _м +  _д . Коэффициент ослабления волны  _д за счет потерь в диэлектрике определяется формулой (2.32).

то

Коэффициент ослабления _м, обусловленный потерями в проводящих пластинах определяется по формуле (2.31) и равен 0,0979 м -1 .

Суммарный коэффициент ослабления:

Определить затухание в однопроводном медном фидере, покрытом слоем полиэтилена ( = 2,3) толщиной  / = 5 мм, при диаметре провода 2r = 4 мм и длине волны  =40 см, если длина фидера l = 1 км.

Решение. Из графика рис.2.3 находим отношение r/r₀ =210 -2 , откуда предельный радиус

Волновое сопротивление фидера — табл.2.4

По формуле (2.33) определяем длину волны, распространяющейся вдоль фидера

По формулам (2.34) и табл.2.4 рассчитываем коэффициент затухания фидера

Ответ: l = 1,2210 -2 10 3 дБ = 12,2 дБ.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Задачи с коаксиальным кабелем