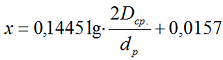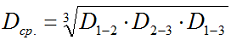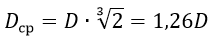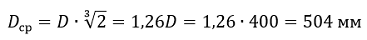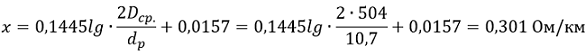Удельное сопротивление нулевой последовательности кабеля таблица ом км

Аврал.Блог

Величина сопротивления нулевой последовательности используется в расчетах однофазного короткого замыкания методом симметричных составляющих. Но, зачастую проблематично найти значение этой величины в справочниках для различного исполнения электрических сетей, и, следовательно, невозможно выполнить расчет. При этом значения сопротивлений фазного и нулевого проводников в справочниках присутствуют. Как же быть?

Можно использовать следующие формулы расчета сопротивления нулевой последовательности:

где R0л (X0л) – активное (индуктивное) сопротивление нулевой последовательности линии;

Rф (Xф) – активное (индуктивное) сопротивление фазного проводника;

Rн (Xн) – активное (индуктивное) сопротивление нулевого проводника.

Вывод формул смотри ниже.

Сразу следует подчеркнуть, что этими формулами следует пользоваться, если сопротивление нулевой последовательности неизвестно. Если есть выбор, использовать справочные данные, или выполнить расчет сопротивления нулевой последовательности, то, наверное, следует отдать предпочтение справочным данным.

Итак, основным документом, регламентирующим расчеты токов короткого замыкания до 1000 В, является ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ». В справочном приложении 2 этого ГОСТ, в таблицах №№ 6-14 содержатся данные о сопротивлениях прямой и нулевой последовательностей для различного исполнения кабельных линий. К сожалению, есть варианты исполнения линий, довольно распространенные, для которых нет подходящей таблицы в этом стандарте. Например, нельзя найти параметры 4-жильного кабеля с алюминиевыми жилами в непроводящей оболочке, если сечение жил одинаковое (в табл.11 сечение нулевого провода меньше, чем сечение фазного). Также, отсутствуют аналогичные данные для кабеля с медными жилами (в табл.14 приведены данные для кабеля в стальной оболочке; да и номенклатура сечений неполная).

В то же время, в справочниках есть данные сопротивлений для любого исполнения линий. Вот только приведены эти данные в виде сопротивлений фазного и нулевого проводников (для применения в расчетах тока однофазного короткого замыкания методом петли «фаза-ноль»), а не сопротивлений прямой, обратной и нулевой последовательностей. Логично предположить, что если результаты расчета по двум разным методам:

• методу петли «фаза-ноль»;
• методу симметричных составляющих,

приравнять, то можно сделать вывод о соотношениях сопротивлений, используемых в этих методах.

Формула расчета тока однофазного КЗ методом петли «фаза-ноль» выглядит следующим образом (см. [2] и [3]):

где U – линейное напряжение сети;

Uф – фазное напряжение сети;

Zпт – полное сопротивление петли фаза-ноль от трансформатора до точки КЗ;

Zс.т. – сопротивление системы и трансформатора току однофазного КЗ

где Х1т, Х2т, Х0т, R1т, R2т, R0т – индуктивные (Х) и активные (R) сопротивления трансформатора токам прямой (1), обратной (2) и нулевой (0) последовательностей;

Хс – индуктивное сопротивление питающей сети;

Rд – сопротивление электрической дуги.

Перепишем формулу (3) в более удобной форме, при этом:

• учтем, что сопротивления прямой и обратной последовательностей равны;
• умножим числитель и знаменатель на 3;
• в знаменателе будем складывать не модули полных сопротивлений, а отдельно их активные и индуктивные составляющие (это сделает расчет более точным).

где Rф (Rн) – активное сопротивление фазного (нулевого) проводника линии;

Xф (Xн) – индуктивное сопротивление фазного (нулевого) проводника линии.

Вот формула расчета тока однофазного КЗ методом симметричных составляющих (см. [1], п.8.2.1, формула 24):

где R1сум. (R0сум.) – суммарное активное сопротивление прямой (нулевой) последовательности;

X1сум. (X0сум.) – суммарное индуктивное сопротивление прямой (нулевой) последовательности.

Перепишем формулу (6), подставив в нее значение фазного напряжения, а также расписав более подробно суммарные величины сопротивлений прямой и обратной последовательностей:

где R1л (R0л) – суммарное активное сопротивление прямой (нулевой) последовательности линии;

X1л (X0л) – суммарное индуктивное сопротивление прямой (нулевой) последовательности линии.

После сравнения формул (5) и (7) получим следующие выражения:

Считая, что Rф=R1л, Xф=X1л, выразим из соотношений (8) и (9) величины сопротивлений нулевой последовательности:

Итак, при отсутствии справочных значений о величине сопротивления нулевой последовательности линии, эти значения можно рассчитать, используя справочные данные сопротивлений фазного и нулевого проводников линии.

Используемая литература

1. ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ».
2. Кужеков С. Л. Практическое пособие по электрическим сетям и электрооборудованию / С.Л. Кужеков, С. В. Гончаров. – Ростов н/Д.: Феникс, 2007.
3. Тульчин И. К., Нудлер Г. И. Электрические сети и электрооборудование жилых и общественных зданий. – 2-е изд., перераб. и доп. – М.: Энерготамиздат, 1990.

Эту статью можно обсудить ниже в комментариях или на форуме.

Источник

Активные и индуктивные сопротивления проводов

В данной статье представлены справочные таблицы активных и индуктивных сопротивлений воздушных линий с проводами из меди, алюминия и стали взятые из ГОСТ, РД, электротехнических справочников и каталогов производителей.

Активные сопротивления проводов

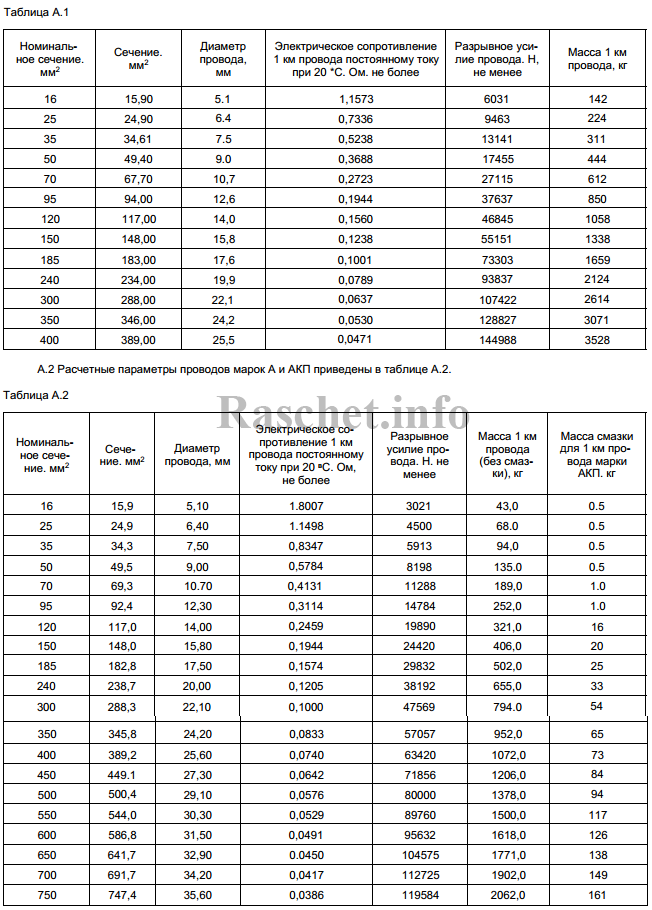
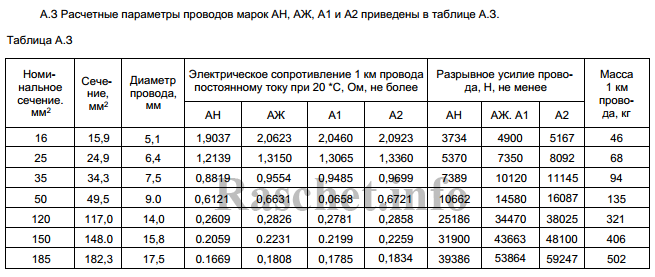
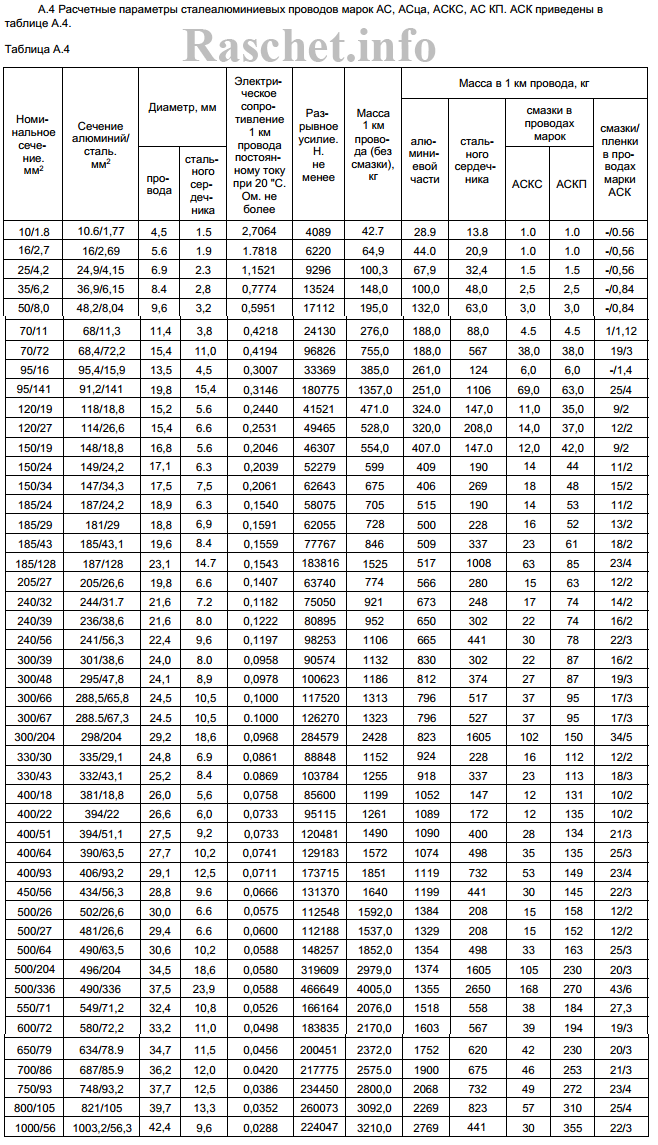
Значения активных сопротивлений проводов марок М, А, АКП, АН, АЖ, А1, А2, АС, АСца, АСКС, АС КП. АСК АТ1С, АТЗС, АТ4С приведены в ГОСТ 839 – 2019 «Провода неизолированные для воздушных линий электропередач» приложение А, таблицы А1 – А8. Для ознакомления, я приведу лишь несколько таблиц из данного ГОСТа, остальные таблицы вы сможете найти непосредственно в самом ГОСТе.

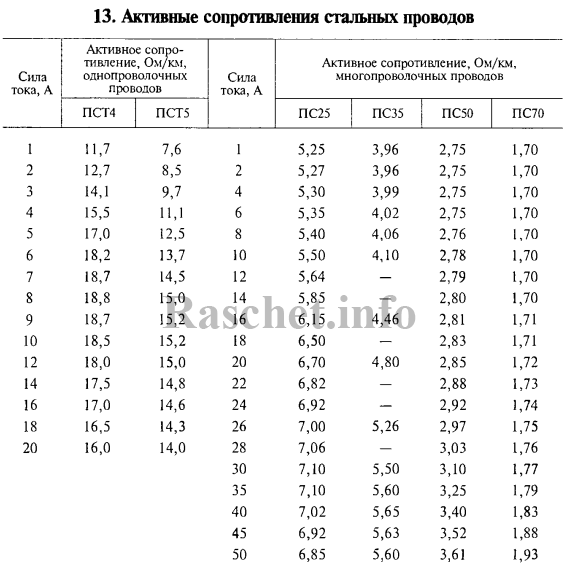
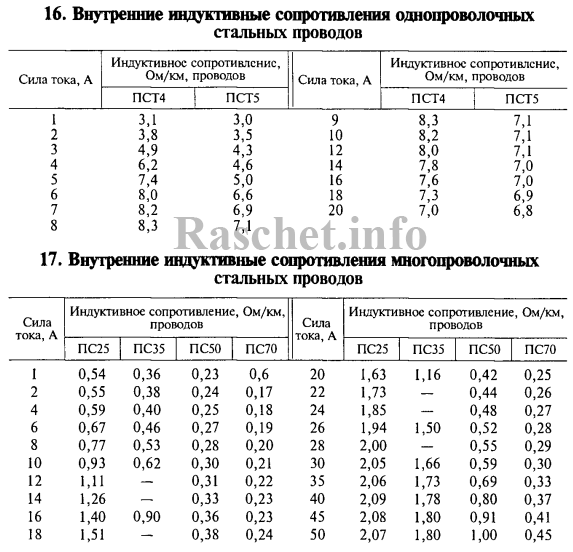
Значения активных сопротивлений стальных проводов марок ПСТ и ПС приведены в книге «Электроснабжение сельского хозяйства. Будзко А.И. 2000 г.» страница 508.

Индуктивные сопротивления проводов

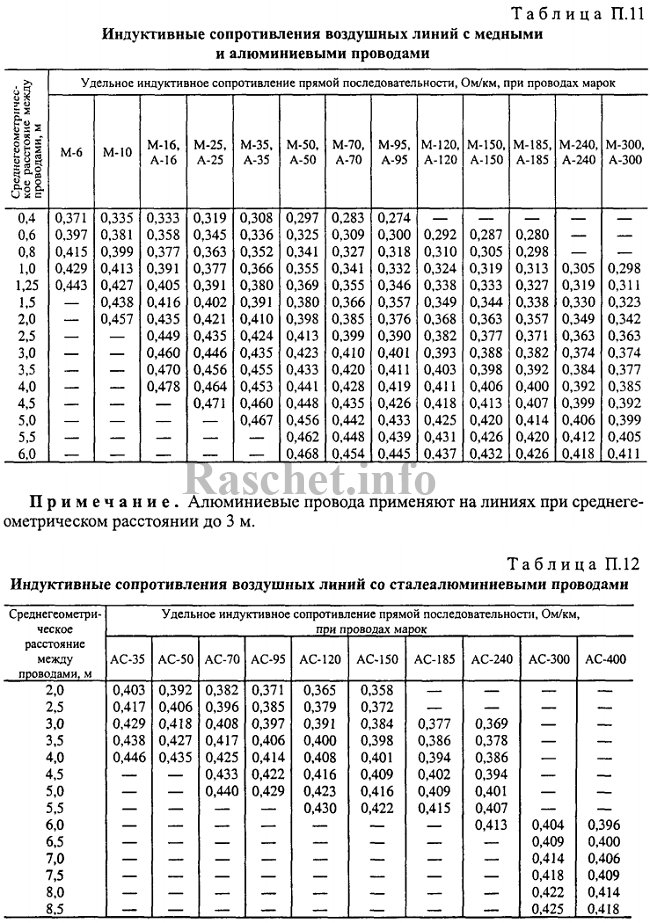
Значения индуктивных сопротивлений для воздушных линий с проводами из меди, алюминия и стали приведены в РД 153-34.0-20.527-98 «Руководящие указания по расчету токов короткого замыкания и выбору электрооборудования» таблицы П1, П2.

Значения индуктивных сопротивлений стальных проводов марок ПСТ и ПС приведены в книге «Электроснабжение сельского хозяйства. Будзко А.И. 2000 г.» страница 511.

Активные и индуктивные сопротивления проводов СИП-1, СИП-2, СИП-4

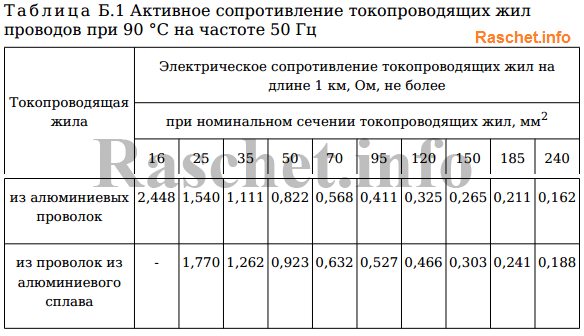
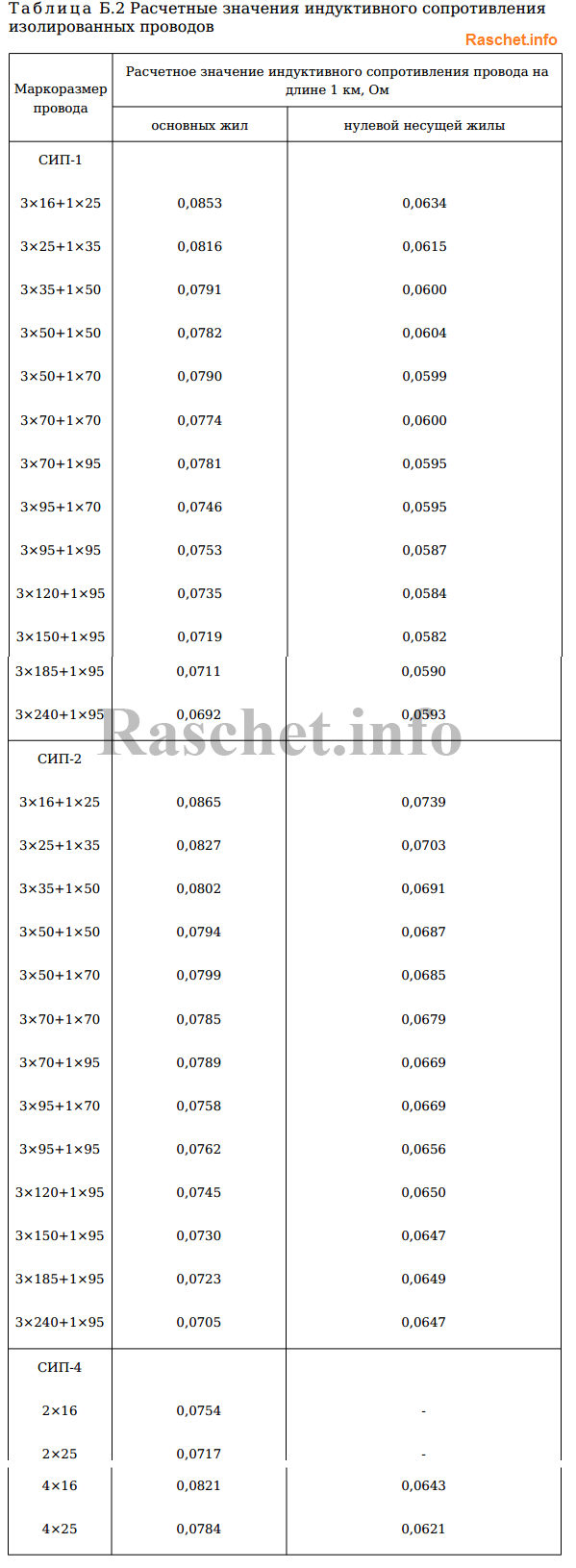
Значения активных и индуктивных сопротивлений для проводов СИП-1, СИП-2 и СИП-4 приведены в ТУ 16-705.500-2006 «Провода самонесущие изолированные и защищенные для воздушных линий электропередач» таблицы Б.1, Б.2.

Активные и индуктивные сопротивления проводов СИП-3

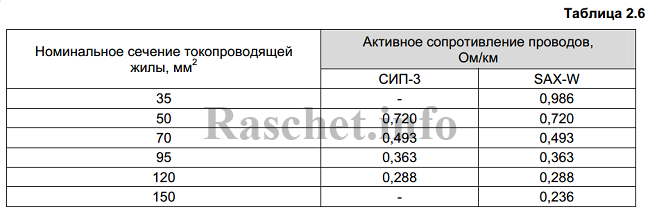
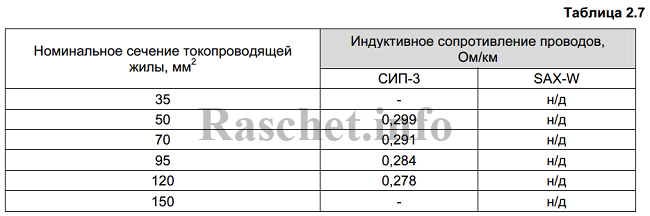
Значения активных и индуктивных сопротивлений для проводов СИП-3(SAX-W) приведены в «Пособии по проектированию воздушных линий электропередачи напряжением 0,38 – 20 кВ с СИП. Книга 4» от компании «ENSTO» таблицы 2.6 и 2.7.

Также значение активных сопротивлений для проводов СИП-3 указаны в ГОСТ 31946—2012 таблица 3. В данной таблице электрическое сопротивление нулевой несущей жилы и токопроводящей жилы указаны при температуре 20 °С.

Как мы видим значения сопротивлений из пособия компании «ENSTO» таблица 2.6 совпадают с ГОСТ 31946—2012 таблица 3.

Значения индуктивных сопротивлений, приведённые в таблице 2.7 указаны для проводов СИП-3 на напряжение 20 кВ с междуфазным расстоянием 400 мм (данное расстояние указано на установочных чертежах в каталоге).

Соответственно если у вас расстояние между проводами не 400 мм и провода используются свыше напряжения 20 кВ, то применять сопротивления из таблицы 2.7 – я не рекомендую.

В этом случае, ориентировочно индуктивное сопротивление можно рассчитать, по формуле [Л1, с.19]:

• Dср. – среднее геометрическое расстояние между проводами, мм;

• D_1-2 — расстояние между проводами первой и второй фазы;
• D_2-3 — расстояние между проводами второй и третей фазой;
• D_1-3 — расстояние между первой и третей фазой.

Если провода расположены в вершинах равностороннего треугольника со стороной D, имеем Dср = D. Для проводов же, расположенных в одной горизонтальной плоскости и удаленных друг от друга на расстояние D, действительно равенство:

• dр – расчетный диаметр токопроводящей жилы провода без учета изоляции (мм), определяется по ТУ 16-705.500-2006;

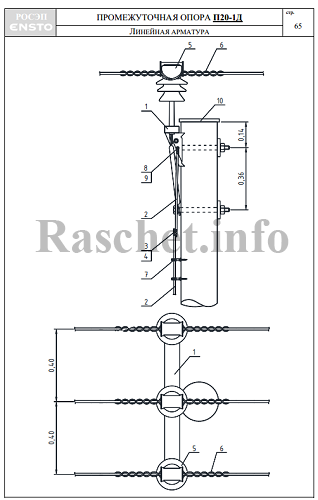
Определить индуктивное сопротивление для проводов марки СИП-3 1х50-20, расположенных в одной горизонтальной плоскости и удаленных друг от друга на расстояние D = 400 мм.

1. Определяем среднее геометрическое расстояние между проводами:

где: D = 400 мм – расстояние между проводами.

2. Определяем индуктивное сопротивление для проводов марки СИП-3 1х50-20:

где: dр = 10,7 мм – расчетный диаметр токопроводящей жилы провода без учета изоляции.

Более подробно с самой методикой расчета можно ознакомиться в статье: «Определение активных и индуктивных сопротивлений проводов» .

Чтобы уменьшить время на постоянные расчеты индуктивного сопротивления проводов СИП-3, используя формулу, приведенную выше, я предварительно выполнил расчеты для наиболее часто используемых расстояний между проводами 400 – 6000 мм и для всех сечений проводов СИП-3 от 1х35 до 1х240 мм2. Полученные значения индуктивных сопротивлений, я свел в таблицы 1 и 2.

Таблица 1 – Индуктивное сопротивление проводов СИП-3-20 кВ

Индуктивное сопротивление проводов СИП-3-20 кВ, Ом/км
Среднее геометрическое расстояние между проводами (Dср.), мм	Число и номинальное сечение фазных жил
	1×35	1×50	1×70	1×95	1×120	1×150	1×185	1×240
	Расчетный наружный диаметр провода, мм (ТУ 16-705.500-2006 — Таблица 2)
	12	13	15	16	18	19	21	24
	ТУ 16-705.500-2006 — Номинальная толщина защитной изоляции защищенных проводов на номинальное напряжение 20 кВ — 2,3 мм, на номинальное напряжение 35 кВ — 3,5 мм.
	Расчетный диаметр токопроводящей жилы без учета изоляции (dр), мм
	9,7	10,7	12,7	13,7	15,7	16,7	18,7	21,7
400	0,293	0,286	0,276	0,271	0,262	0,259	0,251	0,242
450	0,300	0,294	0,283	0,278	0,270	0,266	0,259	0,249
500	0,307	0,300	0,290	0,285	0,276	0,273	0,265	0,256
550	0,313	0,306	0,296	0,291	0,282	0,278	0,271	0,262
600	0,318	0,312	0,301	0,296	0,288	0,284	0,277	0,268
700	0,328	0,322	0,311	0,306	0,298	0,294	0,287	0,277
800	0,336	0,330	0,319	0,314	0,306	0,302	0,295	0,286
900	0,343	0,337	0,327	0,322	0,313	0,309	0,302	0,293
1000	0,350	0,344	0,333	0,328	0,320	0,316	0,309	0,300
1250	0,364	0,358	0,347	0,342	0,334	0,330	0,323	0,314
1500	0,376	0,369	0,359	0,354	0,345	0,341	0,334	0,325
2000	0,394	0,387	0,377	0,372	0,363	0,360	0,352	0,343
2500	0,408	0,401	0,391	0,386	0,377	0,374	0,366	0,357
3000	0,419	0,413	0,402	0,397	0,389	0,385	0,378	0,369
3500	0,429	0,423	0,412	0,407	0,399	0,395	0,388	0,378
4000	0,437	0,431	0,420	0,415	0,407	0,403	0,396	0,387
4500	−	−	0,428	0,423	0,414	0,410	0,403	0,394
5000	−	−	0,434	0,429	0,421	0,417	0,410	0,401
5500	−	−	−	−	0,427	0,423	0,416	0,407
6000	−	−	−	−	−	−	−	0,412

Как мы видим значение индуктивного сопротивления проводов СИП-3 1х50-20 из расчетной таблицы 1 практически совпало со значением из таблицы 2.7 компании «ENSTO».

Таблица 2 — Индуктивное сопротивление проводов СИП-3-35 кВ

Индуктивное сопротивление проводов СИП-3-35 кВ, Ом/км
Среднее геометрическое расстояние между проводами (Dср.), мм	Число и номинальное сечение фазных жил
	1×35	1×50	1×70	1×95	1×120	1×150	1×185	1×240
	Расчетный наружный диаметр провода, мм (ТУ 16-705.500-2006 — Таблица 2)
	14	16	17	19	20	22	24	26
	ТУ 16-705.500-2006 — Номинальная толщина защитной изоляции защищенных проводов на номинальное напряжение 20 кВ — 2,3 мм, на номинальное напряжение 35 кВ — 3,5 мм.
	Расчетный диаметр токопроводящей жилы без учета изоляции (dр), мм
	10,5	12,5	13,5	15,5	16,5	18,5	20,5	22,5
400	0,288	0,277	0,272	0,263	0,259	0,252	0,246	0,240
450	0,295	0,284	0,279	0,271	0,267	0,259	0,253	0,247
500	0,302	0,291	0,286	0,277	0,273	0,266	0,260	0,254
550	0,308	0,297	0,292	0,283	0,279	0,272	0,266	0,260
600	0,313	0,302	0,297	0,289	0,285	0,278	0,271	0,265
700	0,323	0,312	0,307	0,298	0,294	0,287	0,281	0,275
800	0,331	0,320	0,315	0,307	0,303	0,296	0,289	0,283
900	0,339	0,328	0,323	0,314	0,310	0,303	0,297	0,291
1000	0,345	0,334	0,329	0,321	0,317	0,310	0,303	0,297
1250	0,359	0,348	0,343	0,335	0,331	0,324	0,317	0,311
1500	0,371	0,360	0,355	0,346	0,342	0,335	0,329	0,323
2000	0,389	0,378	0,373	0,364	0,360	0,353	0,347	0,341
2500	0,403	0,392	0,387	0,378	0,374	0,367	0,361	0,355
3000	0,414	0,403	0,398	0,390	0,386	0,379	0,372	0,366
3500	0,424	0,413	0,408	0,399	0,395	0,388	0,382	0,376
4000	0,432	0,421	0,416	0,408	0,404	0,397	0,390	0,384
4500	−	−	0,424	0,415	0,411	0,404	0,398	0,392
5000	−	−	0,430	0,422	0,418	0,411	0,404	0,398
5500	−	−	−	−	0,424	0,417	0,410	0,404
6000	−	−	−	−	−	−	−	0,410

1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.

Источник