IT1305: Структурированные кабельные системы
В многомодовом волокне наиболее важным моментом, который ограничивает расстояние связи, является оптическая полоса пропускания.
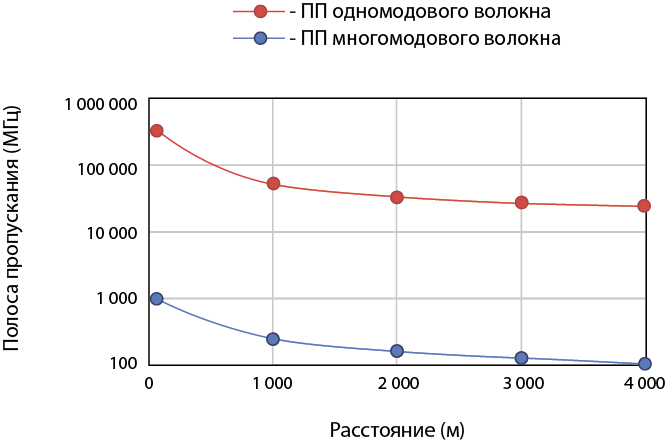
Этот термин употребляется немного неправильно и фактически означает способность передавать информацию. Как и со множеством других оптических параметров, существуют значительные различия между общеупотребительными терминами для коаксиальных кабелей и соответствующими им понятиями для оптических кабелей. Теоретическая ширина спектра сигнала, которая может быть передана по волокну, очень высока — порядка 50-300 ГГц на короткие расстояния. В реальности ширина полосы пропускания в системе определяется длиной волны, оптикой, электроникой, коммутационным оборудованием, волокном и длиной участка. На рис. 84 отображена зависимость ширины полосы пропускания в системе от расстояния кабеля в многомодовых и одномодовых волокнах.
Как вы можете увидеть сами, существует значительная разница в ширине полосы пропускания в системе между многомодовыми и одномодовыми волокнами. Многомодовое волокно, как свидетельствует его название, дает возможность проходить нескольким световым модам, что увеличивает хроматическую и модовую дисперсию. Данная дисперсия светового сигнала значительно ограничивает информационную пропускную способность многомодового волокна. Минимальные стандарты производительности отображены в табл. 11.4.
Полезная ширина полосы пропускания на определенной длине кабеля может быть введена через разделение указанного произведения ширины полосы пропускания и расстояния на реальную протяженность в километрах. Следовательно, в кабеле 50/125 мкм длиной 100 м волокна ширина канала составляет (500 МГц*км) / (ОД км) = 5000 МГц.
Рис. 84 Полоса пропускания оптических систем
С другой стороны, 220 м кабель с 62,5/125 мкм будет иметь эффективную ширину полосы пропускания в 727 МГц, что будет серьезной проблемой для Gigabit Ethernet. Проектировщик системы сталкивается со своего рода дилеммой в вопросе вида оптоволоконного кабеля, который идет от розетки к рабочей станции. С одной стороны, многомодовое волокно значительно дешевле и на данный момент поддерживается большим количеством систем рабочих станций/концентраторов.
Одномодовое волокно имеет гораздо более высокую информационную пропускную способность и может находиться в эксплуатации довольно долгое время. Более того, теперь большая часть оптики оборудования в высокоскоростных сетях строится на лазерных диодах, что сводит на нет выгодную стоимость светодиодных источников, которые хорошо совмещаются с многомодовым волокном.
Следовательно, проблема состоит в том, стоит ли проводить на рабочий стол менее дорогой и более распространенный многомодовый оптический кабель либо использовать одномодовый. Одномодовое волокно имеет свои недостатки, но обладает широкой полосой пропускания, что полезно для будущего развития сетей. Но одномодовое волокно на данный момент несовместимо с большинством оборудования.
Ответ состоит в том, что многие понимают, что можно использовать оба вида. Стандарт требует, чтобы в каждой розетке на рабочем месте было как минимум два кабеля, один из которых оптический. Однако он не запрещает использование более чем двух кабелей на рабочем месте. Почти все модульные блоки позволяют иметь как минимум четыре модульных разъема. Следовательно, оптимальным решением проблемы на сегодняшний день и на будущее будет расположение двух медных кабелей и двух оптических кабелей, одного одномодового и одного многомодового, в каждой розетке. Если вы будете использовать новые оптические коннекторы SFF и медные модули категорий 5е или 6, то ваша система сможет работать со множеством компонентов на протяжении долгих лет.
Таблица 11.4 Информационная пропускная способность многомодового оптического волокна
| Количество мод | Диаметр основы/оболочки, мкм | Рабочая длина волны, нм | Произведение расстояния и полосы пропускания, МГц/км |
|---|---|---|---|
| Многомодовое | 50/125 | 850 | 500 |
| Многомодовое | 50/125 | 1300 | 500 |
| Многомодовое | 62,5/125 | 850 | 160 |
| Многомодовое | 62,5/125 | 1300 | 500 |
Проблема использования лазерного источника VCSEL в многомодовых кабелях
Популярным лазерным источником для высокоскоростных сетей является вертикальный лазер наружного излучения (VCSEL). Этот полупроводниковый диод совмещает высокую пропускную способность с небольшой стоимостью и является идеальным выбором для гигабитных сетей. В одномодовом оптическом кабеле лазерный источник работает безупречно. Его сильно сконцентрированный луч света с легкостью направляется в центр узкой сердцевины одномодового волокна и совершает передачу на одной моде со всеми втекающими плюсами.
Однако, как уже описывалось ранее, большинство оптических кабелей в локальной сети являются многомодовыми. Когда мы использовали светодиодные источники в низкоскоростных технологиях типа 10BaseFL и 100BaseFX, мы требовали, чтобы светодиод нацеливался на передающий конец многомодового волокна, а дальше уже все шло само собой. В этом случае избыточный свет, который не попадал в сердцевину, терялся, но свет, который попадал в нее, распространялся в нем на всех модах (отсюда название «многомодовый»). Метод использования источника света на волокне называется запуском, а применение большего количества света, чем необходимо, — запуском с переполнением.
К сожалению, когда многомодовый кабель создавался, было уделено очень мало внимания небольшим дефектам в сердцевине стекловолокна. Если в волокно запускается много мод, то мелкие нарушения не приносят большого вреда, так как все другие моды (лучи) света проходят внутри просто идеально. В большинстве случаев данные дефекты вызывают лишь небольшое увеличение затухания кабеля. Здесь не о чем беспокоиться, если только не используется лазерный источник.
Помните, что лазер представляет собой очень узкий луч монохроматического света, с шириной спектра 1 мкм для большинства VCSEL, который запускается точно из центральной оси сердцевины волокна. Это значит, что любой даже небольшой дефект может отразить значительное количество лучевой энергии, что вызовет большое затухание. Это может в свою очередь вызывать обрыв связи, если система не способна справляться с потерями дополнительных 2-10 дБ. Более того, минимальные повреждения волокна, которые могут быть вызваны механическими передвижениями и повышениями температур, могут привести к тому, что проблемы со связью будут постоянными.
Существует два решения проблемы VCSEL. Первое состоит в том, чтобы использовать лучшее волокно. Естественно, если вы устанавливаете новый кабель, то это лучший вариант. Вы должны быть уверены, что оптический кабель, используемый вами, подходит для работы с лазером, а также имеет повышенную пропускную способность (произведение пропускной способности на расстояние). Подобное волокно обычно называется gigabit-ready (подходящее для гигабитных скоростей) или совместимым с лазером.
Если у вас есть только многомодовое волокно, вы можете использовать короткий адаптер условного запуска для применения одномодового лазерного источника на многомодовых кабелях. Минус состоит в том, что такой адаптер увеличит стоимость системы на 50-100 долларов. Если вы полагаете, что у вас могут возникнуть проблемы с более старым многомодовым кабелем, то можете продолжать использовать 10BaseSX, так как многие приемопередатчики в этой технологии имеют встроенную настройку моды. Проконсультируйтесь с производителями оборудования на данную тему.
Источник
Реферат: Расчет параметров оптического волокна SM — 9 125 фирмы Lucent Technologies
| Название: Расчет параметров оптического волокна SM — 9 125 фирмы Lucent Technologies Раздел: Рефераты по коммуникации и связи Тип: реферат Добавлен 14:44:41 31 мая 2011 Похожие работы Просмотров: 1810 Комментариев: 19 Оценило: 3 человек Средний балл: 4 Оценка: неизвестно Скачать | |||||||||||||||||||||||||||
а) многомодовое ступенчатое волокно |
 |
в) ступенчатое одномодовое г) одномодовое волокно
волокно (SF) со смещенной дисперсией (DSF)
Рисунок 1 – Типы оптических волокон
Одномодовое волокно имеет значительно меньший диаметр сердцевины по сравнению с многомодовым и, как следствие, из-за отсутствия межмодовой дисперсии, более высокую пропускную способность. Однако оно требует использования более дорогих лазерных передатчиков.
В ВОЛС наиболее широко используются следующие стандарты волокон (таблица 1):
многомодовое градиентное волокно 50/125 (рисунок 1 а);
многомодовое градиентное волокно 62,5/125 (рисунок 1 б);
одномодовое ступенчатое волокно SF (волокно с несмещенной дисперсией или стандартное волокно) 8-10/125 (рисунок 1 в);
одномодовое волокно со смещенной дисперсией DSF 8-10/125 (рисунок 1 г);
одномодовое волокно с ненулевой смещенной дисперсией NZDSF (по профилю показателя преломления это волокно схоже с предыдущим типом волокна).
Таблица 1 – Стандарты оптических волокон и области их применения
| Многомодовое волокно | Одномодовое волокно | |||
| MMF 50/125 градиентное волокно | ||||
| ЛВС (Ethernet, Fast/Gigabit Ethernet, FDDI, ATM) | ЛВС (Ethernet, Fast/Gigabit Ethernet, FDDI, ATM) | Протяженныесети (Ethernet, Fast/Gigabit Ethernet, FDDI, ATM), магистрали SDH) | Сверхпротяженные сети, супермагистрали (SDH, ATM) | Сверхпротяженные сети, супермагистрали (SDH, ATM), полностью оптические сети |
Большинство устройств волоконной оптики используют область инфракрасного спектра в диапазоне от 800 до 1600 нм в основном в трех окнах прозрачности: 850, 1310 и 1550 нм. Именно окрестности этих трех длин волн образуют локальные минимумы затухания сигнала и обеспечивают большую дальность передачи.
Многомодовые градиентные волокна
В стандартном многомодовом градиентном волокне (50/125 или 62,5/125) диаметр светонесущей жилы 50 и 62,5 мкм, что на порядок больше длины волны передачи. Это приводит к распространению множества различных типов световых лучей — мод — во всех трех окнах прозрачности. Два окна прозрачности 850 и 1310 нм обычно используют для передачи света по многомодовому волокну.
В ступенчатом одномодовом волокне (SF) диаметр светонесущей жилы составляет 8-10 мкм и сравним с длиной световой волны. В таком волокне при достаточно большой длиневолны света λ > λ CF ( λ >λ CF – длина волны отсечки) распространяется только один луч (однамода). Одномодовый режим в одномодовом волокне реализуется в окнах прозрачности 1310 и 1550 нм. Распространение только одной моды устраняет межмодовую дисперсию и обеспечивает очень высокую пропускную способность одномодового волокна в этих окнах прозрачности. Наилучший режим распространения с точки зрения дисперсии достигается в окрестности длины волны 1310 нм, когда хроматическая дисперсия обращается в ноль. С точки зрения потерь это не самое лучшее окно прозрачности. В этом окне потери составляют 0,3-0,4 дБ/км, в то время как наименьшее затухание 0,2-0,25 дБ/км достигается в окне 1550 нм.
В одномодовом волокне со смещенной дисперсией (DSF) длина волны, на которой результирующая дисперсия обращается в ноль, – длина волны нулевой дисперсии λ о – смещена в окно 1550 нм. Такое смещение достигается благодаря специальному профилю показателя преломления волокна, рисунок 1 г. Таким образом, в волокне со смещенной дисперсией реализуются наилучшие характеристики как по минимуму дисперсии, так и по минимуму потерь. Поэтому такое волокно лучше подходит для строительства протяженных сегментов с расстоянием между ретрансляторами до 100 и более км. Разумеется, единственная рабочая длина волны берется близкой к 1550 нм.
Одномодовое волокно с ненулевой смещенной дисперсией NZDSF в отличие от DSF оптимизировано для передачи не одной длины волны, а сразу нескольких длин волн (мультиплексного волнового сигнала) и наиболее эффективно может использоваться при построении магистралей «полностью оптических сетей» – сетей, на узлах которых не происходит опто-электронного преобразования при распространении оптического сигнала.
Передача мультиплексного сигнала на большие расстояния требует использования линейных широкополосных оптических усилителей, из которых наибольшее распространение получили так называемые эрбиевые усилители на основе легированного эрбием волокна (EDFA). Линейные усилители типа EDFA эффективно могут усиливать сигнал в своем рабочем диапазоне от 1530-1560 нм. Длина волны нулевой дисперсии у волокна NZDSF, в отличие от волокна DSF, выведена за пределы этого диапазона, что значительно ослабляет влияние нелинейных эффектов в окрестности точки нулевой дисперсии при распространении нескольких длин волн.
Оптимизация трех перечисленных типов одномодовых волокон совершенно не означает, что они всегда должны использоваться исключительно под определенные задачи: SF– передача сигнала на длине волны 1310 нм, DSF– передача сигнала на длине волны 1550 нм, NZDSF– передача мультиплексного сигнала в окне 1530-1560 нм. Так, например, мультиплексный сигнал в окне 1530-1560 нм можно передавать и по стандартному ступенчатому одномодовому волокну SF. Однако длина безретрансляционного участка при использовании волокна SF будет меньше, чем при использовании NZDSF, или иначе потребуется очень узкая полоса спектрального излучения лазерных передатчиков для уменьшения результирующей хроматической дисперсии. Максимальное допустимое расстояние определяется техническими характеристиками как самого волокна (затуханием, дисперсией), так и приемопередающего оборудования (мощностью, частотой, спектральным уширением излучения передатчика, чувствительностью приемника).
1.2 Распространение света по волокну
Основными факторами, влияющими на характер распространения света в волокне, наряду с длиной волны излучения, являются: геометрические параметры волокна; затухание; дисперсия.
Геометрические параметры волокна
Относительная разность показателей преломления. Волокно состоит из сердцевины и оболочки. Оболочка окружает оптически более плотную сердцевину, являющуюся светонесущей частью волокна, рисунок 2.
 |
Рисунок 2 – Ход лучей в многомодовом оптическом волокне со ступенчатым профилем
Будем обозначать через n 1 и n 2 показатели преломления сердцевины и оболочки, соответственно. Один из важных параметров, который характеризует волокно, это – относительная разность показателей преломления Δ :
 |
Если показатель преломления оболочки выбирается всегда постоянной величиной, то показатель преломления сердцевины в общем случае может зависеть от радиуса. В этом случае для проведения различных оценок параметров волокна вместо n 1 используют n 1 eff
Распространение света по волокну можно объяснить на основе принципа полного внутреннего отражения, вытекающего из закона преломления света Снеллиуса:
 |
где n 1 – показатель преломления среды 1, Θ1 – угол падения, n 2 – показатель преломления среды 2, Θ2 – угол преломления.
Формальные выкладки удобнее производить для ступенчатого волокна (волокна со ступенчатым профилем показателя преломления), в котором показатель преломления сердцевины является постоянной величиной (n 1 = const ). На рисунке 2 показан ход лучей в таком волокне. Так как сердцевина является оптически более плотной средой по отношению к оболочке (n 1 > n 2 ), то существует критический угол падения ΘС — внутренний угол падения на границу, при котором преломленный луч идет вдоль границы сред (Θ2 = 90° ). Из закона Снеллиуса легко найти этот критический угол падения:
 |
Если угол падения на границу раздела меньше критического угла падения (луч 2), то при каждом внутреннем отражении часть энергии рассеивается наружу в виде преломленного луча, что приводит в конечном итоге к затуханию света. Если же угол падения больше критического угла (луч 1), то при каждом отражении от границы вся энергия возвращается обратно в сердцевину благодаря полному внутреннему отражению.
Лучи, траектории которых полностью лежат в оптически более плотной среде, называ ются направляемыми. Поскольку энергия в направляемых лучах не рассеивается наружу, такие лучи могут распространяться на большие расстояния.
Числовая апертура. Важным параметром, характеризующим волокно, является числовая апертура NA . Она связана с максимальным углом Θ А вводимого в волокно излучения из свободного пространства, при котором свет испытывает полное внутреннее отражение и распространяется по волокну, формулой: [1]
 |
Фирмы-изготовители волокна экспериментально измеряют угол ΘА и указывают соответствующее значение числовой апертуры для каждого поставляемого типа волокна. Для волокна со ступенчатым профилем легко получить значение числовой апертуры, выраженное через показатели преломления:
 |
Для градиентного волокна используется понятие локальной числовой апертуры значение которой максимально на оси и падает до 0 на границе серд
цевины и оболочки. Для градиентного волокна с параболическим профилем показателя преломления, определяется эффективная числовая апертура, которая равна
(6)
где n 1 (0) — максимальное значение показателя преломления на оси.
Нормированная частота. Другим важным параметром, характеризующим волокно и распространяющийся по нему свет, является нормированная частота V , которая определяется как
 |
где d — диаметр сердцевины волокна. [1]
Номенклатура мод. При более строгом рассмотрении процесса распространения света по волокну следует решать волновые уравнения Максвелла. Именно в этой трактовке лучи ассоциируются с волнами, причем различные типы волн – решения уравнений – называются модами. Сами моды обозначаются буквами Е и/или Н с двумя индексами n иm (Еnm и Нnm ). Индекс n характеризует азимутальные свойства волны (число изменений поля по окружности), am — радиальные (число изменений поля по диаметру). По оптическому волокну распространяются только два типа волн: симметричные (Е0 m и Н0 m ), у которых только одна продольная составляющая, и несимметричные (смешанные) (Enm и Hnm ), у которых имеется две продольные составляющие. При этом, если преобладает продольная составляющая электрического поля – Ez , то волна обозначается EHnm , а если преобладает продольная составляющая магнитного поля – Hz , то волна называется HEnm . Сопоставляя волновую теорию с геометрической оптикой, следует отметить, что симметричные моды Е0 m и Н0 m соответствуют меридиональным лучам, несимметричные моды Enm и Hnm – косым лучам.
По волокну могут распространяться как только одна мода – одномодовый режим, так и много мод – многомодовый режим. Многомодовый или одномодовый характер идущего по волокну света коренным образом влияет на дисперсию, а следовательно, и на пропускную способность волокна. Расчет на основе уравнений Максвелла позволяет найти простой критерий распространения одной моды:
V -4 и сильней проявляются в области коротких длин волн.
Длина волны, на которой достигается нижний предел собственного затухания чистого кварцевого волокна, составляет 1550 нм и определяется разумным компромиссом между потерями вследствие рэлеевского рассеяния и инфракрасного поглощения.
На рисунке 5 приводится общий вид спектральной зависимости собственных потерь с указанием характерных значений четырех основных параметров (минимумов затухания в трех окнах прозрачности 850, 1300 и 1550 нм, и пика поглощения на длине волны 1480 нм) для современных одномодовых и многомодовых волокон.
 |
Рисунок 5 – Собственные потери в оптическом волокне [2]
Кабельные (радиационные) потери αrad обусловлены скруткой, деформациями и изгибами волокон, возникающими при наложении покрытий и защитных оболочек, производства кабеля, а так же в процессе инсталляции ВОК. При соблюдении ТУ на прокладку кабеля номинальный вклад со стороны радиационных потерь составляет не больше 20% от полного затухания. Дополнительные радиационные потери появляются, если радиус изгиба кабеля становится меньше минимального радиуса изгиба, указанного в спецификации на ВОК.
Дисперсия и полоса пропускания
По оптическому волокну передается не просто световая энергия, но также полезный информационный сигнал. Импульсы света, последовательность которых определяет информационный поток, в процессе распространения расплываются. При достаточно большом уши-рении импульсы начинают перекрываться, так что становится невозможным их выделение при приеме.
Дисперсия – уширение импульсов – имеет размерность времени и определяется как квадратичная разность длительностей импульсов на выходе и входе кабеля длины L по формуле
 |
Обычно дисперсия нормируется в расчете на 1 км, и измеряется в пс/км. Дисперсия в общем случае характеризуется тремя основными факторами, рассматриваемыми ниже:
• различием скоростей распространения направляемых мод (межмодовой дисперсией τмод ),
• направляющими свойствами световодной структуры (волноводной дисперсией τ w ),
• свойствами материала оптического волокна (материальной дисперсией τ mat ).
 |
Рисунок 6 – Основные виды дисперсии
Чем меньше значение дисперсии, тем больший поток информации можно передать по волокну. Результирующая дисперсия τ определяется из формулы
(15)
Межмодовая дисперсия возникает вследствие различной скорости распространения мод, и имеет место только в многомодовом волокне (рисунок 3 а, б). Для ступенчатого многомодового волокна и градиентного многомодового волокна с параболическим профилем показателя преломления ее можно вычислить соответственно по формулам
 |
где Lc — длина межмодовой связи (для ступенчатого волокна порядка 5 км, для градиентного — порядка 10 км).
Изменение закона дисперсии с линейного на квадратичный связано с неоднородностями, которые есть в реальном волокне. Эти неоднородности приводят к взаимодействию между модами, и перераспределению энергии внутри них. При L > Lc наступает установившийся режим, когда все моды в определенной установившейся пропорции присутствуют в излучении. Обычно длины линий связи между активными устройствами при использовании многомодового волокна не превосходят 2 км и значительно меньше длины межмодовой связи. Поэтому можно пользоваться линейным законом дисперсии.
Вследствие квадратичной зависимости от Δ значения межмодовой дисперсии у градиентного волокна значительно меньше, чем у ступенчатого, что делает более предпочтительным использование градиентного многомодового волокна в линиях связи.
На практике, особенно при описании многомодового волокна, чаще пользуются термином полоса пропускания. При расчете полосы пропускания W можно воспользоваться формулой
(17)
Измеряется полоса пропускания в МГц·км. Из определения полосы пропускания видно, что дисперсия накладывает ограничения на дальность передачи и верхнюю частоту передаваемых сигналов. Физический смысл W — это максимальная частота (частота модуляции) передаваемого сигнала при длине линии 1 км. Если дисперсия линейно растет с ростом растояния, то полоса пропускания зависит от расстояния обратно пропорционально.
Хроматическая дисперсия состоит из материальной и волноводной составляющих и имеет место при распространении как в одномодовом, так и в многомодовом волокне. Однако наиболее отчетливо она проявляется в одномодовом волокне из-за отсутствия межмодовой дисперсии.
Материальная дисперсия обусловлена зависимостью показателя преломления волокна от длины волны. В выражение для дисперсии одномодового волокна входит дифференциальная зависимость показателя преломления от длины волны:
 |
Волноводная дисперсия обусловлена зависимостью коэффициента распространения моды от длины волны
(19)
где введены коэффициенты М(λ) и N ( λ ) – удельные материальная и волноводная дисперсии соответственно, а Δλ , (нм) – уширение длины волны вследствие некогерентности источника излучения. Результирующее значение коэффициента удельной хроматической дисперсии определяется как D ( λ ) = М(λ) + N ( λ ) . Удельная дисперсия имеет размерность пс/(нм·км). Если коэффициент волноводной дисперсии всегда больше нуля, то коэффициент материальной дисперсии может быть как положительным, так и отрицательным. И здесь важным является то, что при определенной длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация М(λ) и В(λ) , а результирующая дис персия D ( λ ) обращается в ноль. Длина волны, при которой это происходит, называется дли ной волны нулевой дисперсии λ0 . Обычно указывается некоторый диапазон длин волн, в пределах которых может варьироваться λ0 для данного конкретного волокна.
Фирма Corning использует следующий метод определения удельной хроматической дисперсии. Измеряются задержки по времени при распространении коротких импульсов света в волокне длиной» не меньше 1 км. После получения выборки данных для нескольких длин волн из диапазона интерполяции (800-1600 нм для MMF, 1200-1600 нм для SF и DSF) делается повторная выборка измерения задержек на тех же длинах волн, но только на коротком эталонном волокне (длина 2 м). Времена задержек, полученных на нем, вычитаются из соответствующих времен, полученных на длинном волокне.
Для одномодового ступенчатого и многомодового градиентного волокна используется эмпирическая формула Селмейера: τ(λ) = А + Вλ 2 + С λ -2 . Коэффициенты А , В , С являются подгоночными, и выбираются так, чтобы экспериментальные точки лучше ложились на кривую τ(λ) , рисунок 7. Тогда удельная хроматическая дисперсия вычисляется по формуле:
 |
где λ0 = (С/В) 1/4 – длина волны нулевой дисперсии, новый параметр So =8В – наклон нулевой дисперсии (paзмepность пс/(нм 2 ·км)), а λ – рабочая длина волны, для которой определяется удельная хроматическая дисперсия.
 |
Рисунок 7 – Кривые временных задержек и удельных хроматических дисперсий для: а) многомодового градиентного волокна (62,5/125);
б) одномодового ступенчатого волокна (SF);
в) одномодового волокна со смещенной дисперсией (DSF)
Поляризационная модовая дисперсия
Поляризационная модовая дисперсия τ pmd – возникает вследствие различной скорости распространения двух взаимно перпендикулярных поляризационных составляющих моды. Коэффициент удельной дисперсии Т нормируется в расчете на 1 км и имеет размерность (пс /
), aτ pmd растет с ростом расстояния по закону 
. Для учета вклада в результирующую дисперсию следует добавить слагаемое 
в правую часть (15). Из-за небольшой величины τpmd может проявляться исключительно в одномодовом волокне, причем когда используется передача широкополосного сигнала (полоса пропускания 2,4 Гбит/с и выше) с очень узкой спектральной полосой излучения 0,1 нм и меньше. В этом случае хроматическая дисперсия становится сравнимой с поляризационной модовой дисперсией.
В одномодовом волокне в действительности может распространяться не одна мода, а две фундаментальные моды – две перпендикулярные поляризации исходного сигнала. В идеальном волокне, в котором отсутствуют неоднородности по геометрии, две моды распространялись бы с одной и той же скоростью, рисунок 8 а. Однако на практике волокна имеют не идеальную геометрию, что приводит к различной скорости распространения двух поляризационных составляющих мод, рисунок 8 б.
 |
Рисунок 8 – Появление поляризационной модовой дисперсии.
Избыточный уровень τ pmd , проявляясь вместе с чирпированным модулированным сигналом от лазера, а также поляризационной зависимостью потерь, может приводить к временным колебаниям амплитуды аналогового видеосигнала. В результате ухудшается качество изображения, или появляются диагональные полосы на телевизионном экране. При передаче цифрового сигнала высокой полосы (>2,4 Гбит/с) из-за наличия τ pmd может возрастать битовая скорость появления ошибок.
Главной причиной возникновения поляризационной модовой дисперсии является нециркулярность (овальность) профиля сердцевины одномодового волокна, возникающая в процессе изготовления или эксплуатации волокна. При изготовлении волокна только строгий контроль позволяет достичь низких значений этого параметра.
2 РАСЧЕТ ПАРАМЕТРОВ ОПТИЧЕСКОГО ВОЛОКНА SM — 9/125 ФИРМЫ LUCENT TECHNOLOGIES
2.1 Расчет геометрических параметров оптоволокна
Числовую апертуру волокна рассчитаем по формуле (5). Подставив значения n 1 =1,466 , Δ=0,33 % , получим:
Далее из выражения (7) найдем нормированную частоту для окна прозрачности λ=1310 нм:
Таким образом, на длине волны 1310 нм (в соответствии с соотношением (8)) в волокне может существовать многомодовый режим, но, как уже говорилось выше, неосновные моды быстрее затухают и при помещении волокна в кабель, который при прокладке будет испытывать изгибы, неосновные моды вырождаются и в волокне будет одномодовый режим.
2.2 Определение длины волны отсечки
Как уже говорилось выше, различают волоконную и кабельную длину волны отсечки. Кабельная определяется экспериментально. Рассчитаем волоконную длину волны отсечки из выражения (12).
нм
Учитывая, что кабельная длина волны отсечки смещена относительно волоконной в сторону более коротких длин волн, это еще раз подтверждает, что на длине волны 1310 нм в волокне, помещенном в кабель будет одномодовый режим.
2.3 Определение затухания в оптоволокне
Как уже писалось выше затухание в волокне складывается из собственных и кабельных потерь. Собственные потери определим из графика на рисунке 5.
дБ/км
Тогда кабельные потери можно определить, как
дБ/км
Общее затухание в волокне составит
дБ/км
Как видно из графика (рисунок 5) наименьшего значения этого показателя можно добиться при работе на длине волны 1550 нм.
2.4 Определение дисперсии и полосы пропускания волокна
Для одномодового режима модовая составляющая дисперсии обращается в 0 . Кроме того, как видно из рисунка 7 б, хроматическая дисперсия в окне прозрачности 1310 нм тоже равна 0 . Таким образом, в этом режиме в волокне будет присутствовать только поляризационная модовая дисперсия. Исходя из технических характеристик оптоволокна коэффициент поляризационной модовой дисперсии составляет Т=0,2 пс/√км. Тогда при расчете на L =100 км длины волокна, получим
пс
Далее из выражения (17) найдем полосу пропускания оптоволокна с расчетом на длину 100 км
Гц
С учетом того, что по техническим характеристикам оптоволокна коэффициент поляризационной модовой дисперсии не превышает значения 0,2 пс/√км, величина W =220 ГГц является минимальной полосой пропускания на расстоянии 100 км.
В курсовом проекте был произведен расчет основных параметров оптического волокна SM — 9/125 фирмы LucentTechnologies для окна прозрачности 1310 нм и регенерационного участка 100 км.
На основании расчетов очевидно, что с точки зрения затухания, для одномодовых волокон является оптимальным режим распространения в окне 1550 нм.
Проведенные расчеты показали, что на длине волны 1310 нм дисперсия является наименьшей (ввиду нулевой хроматической дисперсии и отсутствия модовой дисперсии), что и определило его использование в магистральных линиях связи.
Кроме того, из расчетов видно, что в окне прозрачности 1310 нм в одномодовом волокне может существовать многомодовый режим, но с учетом помещения волокна в кабель, который при прокладке неизбежно претерпевает изгибы, неосновные моды вырождаются, и устанавливается одномодовый режим.
К вышесказанному еще можно добавить что в качестве основного стандарта оптических волокон для наземных магистральных линий связи компанией ОАО «Ростелеком» был выбран стандарт ITU-TG.652, то есть одномодовые оптические волокна в окне прозрачности 1310 нм. [3]
Источник
