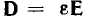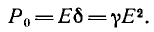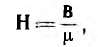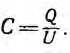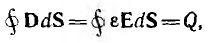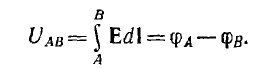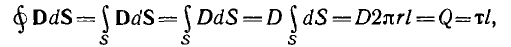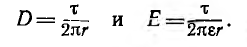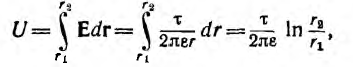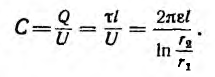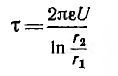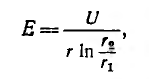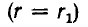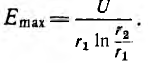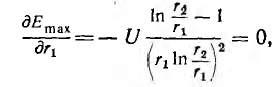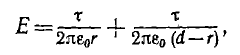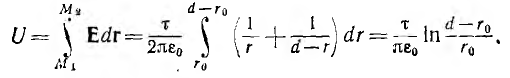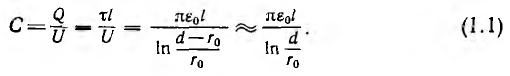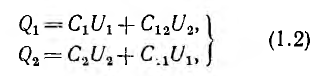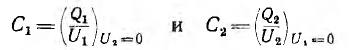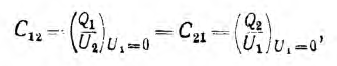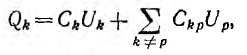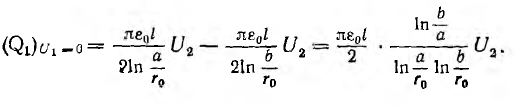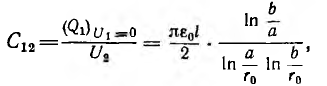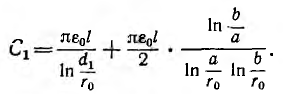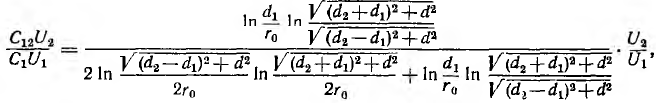Индуктивность коаксиального кабеля
Коаксиальный кабель представляет собой два длинных соосных проводящих цилиндра, пространство между которыми заполнено каким-либо изолирующим материалом с магнитной проницаемостью m. Пусть а — радиус внутреннего цилиндра, а b — внешнего. Длина кабеля обычно во много раз превышает его радиус. Поэтому магнитное поле, создаваемое электрическим током в кабеле, будет таким же как у бесконечно длинного кабеля, если не учитывать искажения поля у его концов.
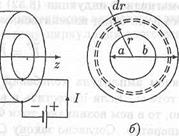
Найдем индуктивность участка кабеля длиной l. Для этого создадим замкнутую электрическую цепь из внутреннего и внешнего цилиндров кабеля и подключим к этой цепи источник постоянной ЭДС (рис. 8.6, а).Токи, создаваемые этой ЭДС, потекут по поверхностям цилиндров вдоль их оси в противоположных направлениях.
В силу цилиндрической симметрии системы силовые линии магнитного поля суть семейство окружностей, центры которых лежат на оси симметрии. На рис. 8.6, а изображена одна из силовых линий. Для определения напряженности магнитного поля применим теорему (7.7) о циркуляции вектора Н . В качестве контура интегрирования С выберем силовую линию произвольного радиуса г. Циркуляция вектора напряженности по такому контуру буд



 |
 |
 |
Рис. 8.6. Коаксиальный кабель
Если радиус контура С меньше радиуса внутреннего цилиндра (г 6), сумма токов равна нулю, так как токи в цилиндрах имеют противоположные направления. Поэтому напряженность магнитного поля Я = 0 при г Ь, т.е. магнитное поле внутри малого цилиндра и вне большого отсутствует. Если радиус контура С таков, что а 2 = (1/2) m I 2 /8p 2 r 2 . (8.35)
Найдем энергию магнитного поля внутри кабеля. Для этого рассмотрим цилиндрический слой, образованный двумя воображаемыми цилиндрами радиусов r и r + dr (рис. 8.6, б).Если длина слоя равна l, то его объем dV = 2prldr. Так как плотность энергии (8.35) зависит только от г, внутри тонкого цилиндрического слоя она будет всюду одна и та же. Поэтому энергия магнитного поля в слое
Проинтегрировав это выражение по r в пределах от а до b, найдем энергию магнитного поля на участке кабеля длиной l:
W = (1/4p) m I 2 l 
С другой стороны, энергию магнитного поля можно определить по формуле (8.26). Приравняем эти выражения и найдем индуктивность участка коаксиального кабеля длиной l:
Взаимная индукция
Рассмотрим два контура с токами I1 и I2 (рис. 8.7), расположенные на некотором расстоянии друг от друга. Ток в первом контуре создает магнитное поле, поток yкоторого через второй контур, очевидно, пропорционален силе тока I2
Аналогично, магнитный поток Ф1 через первый контур поля, создаваемого током во втором контуре, пропорционален силе тока I2.
Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью, или коэффициентами взаимной индукции. Они зависят от формы, размеров, взаимного расположения контуров и от магнитной проницаемости среды, в которой находятся контуры.
 |
Рис. 8.7. Взаимная индукция
Рассмотрим простой пример. Пусть на одном цилиндрическом каркасе имеется две обмотки, образующие два соленоида одинаковой длины l(рис. 8.8). Число витков одного соленоида равно N1, а второго — N2. Найдем коэффициенты L12 и L21 для этой системы.
 |
Рис. 8.8. К вычислению коэффициента взаимной индукции
редположим, что в первом соленоиде течет ток I1, а во втором — 12. В силу (7.17) напряженность магнитного поля тока h внутри соленоида
Поток магнитной индукции этого поля через один из витков 2 соленоида
Так как поле внутри соленоида однородно, потоки через все витки одинаковы. Поэтому потокосцепление
Аналогично, напряженность поля, создаваемого током I2, будет
Поток магнитной индукции этого поля через один из витков первого соленоида
Отсюда найдем, что
Это равенство справедливо для двух любых контуров и составляет содержание теоремы взаимности.
Вычислим энергию магнитного поля двух соосных соленоидов. Векторы напряженности полей, создаваемых токами I1 и I2, внутри соленоидов коллинеарны. Если токи I1 и I2 текут в одном направлении, то векторы H1 и Н2 сонаправлены. В этом случае суммарное магнитное поле характеризуется напряженностью:
Если же токи I1 и I2 текут в разных направлениях, то векторы Н1 и H2 направлены противоположно друг другу. При этом модуль напряженности магнитного поля
Энергию однородного магнитного поля найдем по формуле (8.28):
При помощи формул (8.22) и (8.40), запишем это выражение так:
где первое слагаемое есть энергия тока в первом соленоиде, второе -энергия тока во втором, а третье слагаемое называется взаимной энергией. Формула (8.42) справедлива в общем случае для двух произвольных контуров.
Задача. Найти взаимную индуктивность тороидальной катушки и проходящего по ее оси бесконечного прямого провода. Катушка имеет прямоугольное сечение. Внутренний радиус тороида равен а, внешний —b, а его высота — h. Число витков в катушке — N. Магнитная проницаемость окружающей среды — m.
Источник
Электрическая ёмкость и ее расчет
Содержание:
Электротехника и ее теоретические основы:
Одной из основных задач техники является преобразование при родных энергетических запасов в используемые виды энергии — в механическую, тепловую, световую и т. п., что требует транспортировки энергетического сырья к месту его использования.
Электрическая энергия легко передается на большие: расстояния и с высоким коэффициентом полезного действия преобразуется в другие виды энергии. Общепринятым является преобразование природных энергетических запасов в электрическую энергию с помощью так называемых генераторов и ее передача посредством проводов к месту потребления, где в преобразователях и приемниках она преобразуется в нужный вид энергии. Беспроводная передача энергии осуществляется с помощью радиосвязи.
Преимущества генерирования, передачи, распределения и преобразования электрической энергии обеспечили широкое применение электротехники.
Новые производственные отношения в нашей стране, отсутствие частной собственности на запасы энергетического сырья, средства и орудия производства, государственное планирование являются мощным фактором развития электротехники и всеобъемлющего охвата ею всех отраслей нашего народного хозяйства, быта и культуры.
Составленный под руководством В. И. Ленина план ГОЭЛРО построения 30 электростанций общей мощностью 1,75 млн. кет был выполнен в решающих позициях за 10 лет.
В послевоенные годы электрификация СССР развивается невиданными темпами: в 1960 г. мощность электростанций составила 66,7 млн. кет, а за пятилетку 1966— 1970 гг. введены 54 млн. кет, в том числе самая мощная в мире Красноярская гидроэлектростанция (6 млн. кет) и Белоярская атомная электростанция (600 тыс. кет). В Директивах XXIV съезда КПСС по пятилетнему плану развития народного хозяйства СССР на 1971— 1975 гг. предусмотрено ввести в действие электростанции мощностью 65—67 млн. кет, в том числе 6—8 млн. кет на атомных электростанциях. Соответственно увеличилась и увеличится мощность потребителей — устройств, преобразующих электрическую энергию в другие виды.
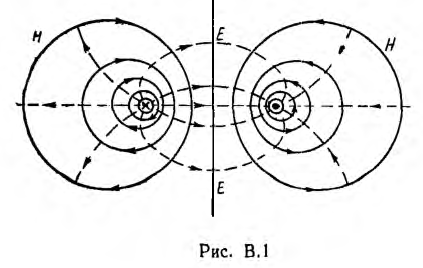
Электрическая энергия — это энергия электромагнитного поля, являющегося видом материи. Поле имеет две составляющие — электрическое и магнитное поля, что можно показать на примере линии передачи постоянного тока (рис. В. 1).
При передаче энергии провода линии, изолированные друг от друга, находятся под напряжением U. Следовательно, между проводами возникает электрическое поле, изображенное пунктиром на рис. В.1 в виде силовых линий, В проводах протекает ток 7, следовательно, в проводах и вне их создается магнитное поле, показанное сплошными линиями. На рис. В.1 видно характерное различие между электрическим и магнитным полями: силовые линии электрического поля незамкнуты, они начинаются и оканчиваются на заряженных проводах; магнитные силовые линии всегда замкнуты; они не имеют ни начала, ни конца.
Как известно из курса физики, электрическое поле в каждой точке
характеризуется вектором напряженности Е, равным силе, воздействующей на единичный положительный заряд, помещенный в эту точку, и вектором электрического смещения
Электрическое поле в проводящей среде создает ток, характеризуемый в
каждой точке поля вектором плотности тока 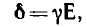
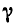
проводимость среды. Ток сопровождается появлением магнитного поля и переходом части энергии электромагнитного поля в тепло, причем мощность этого процесса в единице объема
Магнитное поле в каждой точке характеризуется вектором магнитной индукции В, величина которого равна силе, действующей на движущийся единичный положительный заряд, скорость которого равна единице, а направление В — перпендикулярно этой силе и скорости, а также вектором напряженности
где 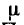
Передача, генерирование, преобразование и потребление электрической энергии, равной 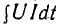
В науке об электричестве связь электрических и магнитных явлений была установлена в двадцатых годах прошлого века, когда Ампер и Эрстед доказали, что электрический ток сопровождается возникновением магнитного поля; окончательно связь электрического и магнитного полей была подтверждена Фарадеем, открывшим явление электромагнитной индукции (1831 г.).
Электротехника, зародившаяся в тридцатых годах прошлого века, вначале развивалась как техника постоянного тока. Только после создания М. О. Доливо-Добровольским системы трехфазного тока и трехфазного двигателя (1891 г.) переменный ток стал вытеснять постоянный. Передача электрической энергии стала осуществляться также трехфазным током.
Теория электромагнитного поля в законченной математической форме была создана Максвеллом в 1873 г. Подтвержденная многочисленными опытами ряда ученых, она была окончательно принята в начале нашего века.
Введенное Максвеллом представление об электромагнитных волнах, экспериментально подтвержденное работами Герца, позволило А. С. Попову в 1895 г. осуществить передачу сигнала без проводов, что послужило началом новой области электротехники — радиотехники.
Электротехника и ее теоретические основы непрерывно развиваются. Например, совершенствуются электронные, ионные и полупроводниковые приборы и аппараты, с помощью которых осуществляют прямые и обратные преобразования переменного тока в постоянный, усиление напряжения и мощности и создают электронные вычислительные машины. Увеличивается дальность и возможности проводной связи, радиотехники и телевидения, развивается электроавтоматика, в энергетике осуществляется переход к большим напряжениям (1500 кв) и мощностям генераторов (1 200 ООО кет и выше), разрабатываются и испытываются магнитогидродинамические прямые преобразователи тепловой энергии в электрическую и т. д.
Так как все электротехнические устройства основаны на использовании электромагнитного поля их систем, состоящих из заряженных тел и контуров с токами, для решения многих задач необходимо привлечение теории этого поля со сложными математическими зависимостями. Однако в большинстве устройств используются ограниченные пути электрического тока и магнитного потока — изолированные проводники малого сопротивления и магнитопроводы из материала с высокой магнитной проницаемостью, называемые электрическими и магнитными цепями. Их расчеты могут быть значительно упрощены, так как не требуют знания составляющих поля в каждой точке устройств. Теория этих цепей основана на использовании интегральных величин: напряжения 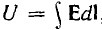
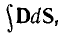
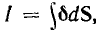
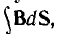
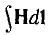
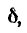
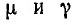
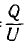
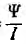
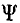
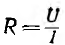
Эти величины можно называть параметрами цепей.
Если эти параметры не зависят от токов и напряжений, уравнения теории цепей, связывающие интегральные величины, будут линейными; такие цепи называют линейными.
В ряде случаев, весьма важных для современной электротехники, эти параметры являются функциями напряжений и токов; тогда уравнения и цепи становятся н нелинейными.
Осуществление грандиозных планов дальнейшей электрификации нашей страны, эксплуатация существующих и создание новых электротехнических устройств требуют от инженера-электрика глубокого понимания физических процессов и умения производить их технический расчет. Фундаментом электротехнического образования является курс теоретических основ электротехники (ТОЭ), базирующийся на сведениях, сообщенных в курсах физики, математики и механики.
Настоящее учебное пособие ТОЭ построено в соответствии с изложенным. Вначале даны параметры цепей, потом основы теории источников и приемников электрической энергии. Затем следует анализ электрических и магнитных цепей при постоянном и переменном токе — линейных и на их основе нелинейных. Курс завершается теорией постоянного и переменного электромагнитного поля.
В книге принята Международная система единиц СИ и рационализованная форма написания уравнений, предложенная Хевисайдом, в которой основные соотношения для электрического и магнитного полей имеют симметричный вид, а множители 4 π и 2 π входят лишь в те соотношения, где они соответствуют характеру симметрии — сферической (4 π) и осевой (2 π).
Параметры электрических и магнитных цепей
Электрической цепью называется совокупность устройств, состоящая из источников, преобразователей и приемников электрической энергии и соединяющих их проводов, образующих замкнутые пути для электрического тока.
Часть цепи, не содержащая источников электрической энергии, называется пассивной, а часть цепи, содержащая источники, называется активной.
Как было показано во введении на примере линии передачи, электрическая цепь характеризуется тремя параметрами: сопротивлением R, емкостью С и индуктивностью L. Этими параметрами обладают все элементы цепей, например резисторы, в которых основную роль играет их сопротивление, конденсаторы с основным параметром — емкостью, и катушки индуктивности, в которых основной является их индуктивность.
Из изложенного вo введении очевидно, что параметры линии передачи равномерно распределены по всей длине линии. Параметры распределены также в отдельных элементах цепи. Например, в катушке индуктивности сопротивление, индуктивность и емкость распределены по ее длине, так как каждый виток с током имеет сопротивление и создает магнитное поле, а отдельные витки изолированного проводника обладают друг по отношению к другу некоторой емкостью.
Этим свойством обладают все реальные электрические цепи—они являются цепями с распределенными параметрами. Так как в ряде технически важных задач не требуется знания электромагнитных процессов в каждой точке всей цепи и ее элементов, необходимо учесть только их интегральные свойства; такие цепи могут быть представлены в виде цепей с сосредоточенными параметрами, состоящих из сопротивлений, индуктивностей и емкостей. Например, катушка индуктивности может быть представлена в виде схемы с последовательным соединением сопротивления R, индуктивности L и с параллельно приключенной к ним емкостью С.
При включении цепи на постоянное напряжение в течение короткого времени от источника потребляется энергия на создание электромагнитного поля. После этого запасенная в С и L энергия сохраняет свою величину неизменной и не отражается на работе цепи, а источники доставляют энергию только на покрытие тепловых потерь в сопротивлениях. Поэтому при расчете цепей постоянного тока следует учитывать только сопротивление R.
В цепях переменного тока энергия, запасаемая в С и L, и мощность потерь в R непрерывно изменяются. Поэтому при расчете этих цепей необходимо учитывать все три параметра.
Многие электрические цепи нелинейны. Так, например, температура, а следовательно, и сопротивление проводника при прохождении по нему тока изменяются; индуктивность катушки со стальным сердечником зависит от тока, так как с величиной тока будет меняться магнитная проницаемость р, сердечника, а следовательно, и индуктивность L. Однако в большинстве случаев цепи можно рассматривать как линейные, считая параметры R, L и С постоянными.
В устройствах современной электротехники главным образом используется энергия магнитного поля, поэтому их основным параметром является индуктивность L. Для этих устройств вводится понятие магнитной цепи как совокупности тел, большей частью ферромагнитных, в которых создается магнитный поток.
При постоянном токе методы анализа магнитных цепей аналогичны методам расчета электрических цепей, содержащих лишь один параметр — сопротивление R. Его аналогом в магнитных цепях является магнитное сопротивление 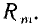
Эта глава посвящена элементарным методам расчета параметров устройств, поля которых имеют простые виды симметрии. Более сложные случаи рассматриваются в теории электромагнитного поля.
Электрическая ёмкость и ее расчет
Для электрических цепей наибольший интерес представляет система двух проводящих тел в диэлектрической среде, заряды + Q и —Q которых отличаются только знаком, являющаяся по существу конденсатором. Емкость конденсатора равна отношению его заряда Q, под которым понимается абсолютное значение разноименных зарядов, к напряжению U между обкладками:
Емкость конденсатора, определяемая размерами и формой тел и их взаимным расположением, пропорциональна диэлектрической проницаемости е среды между обкладками. Емкость измеряется Б фарадах (ф), заряд в кулонах (к), напряжение в вольтах (в).
Для расчета емкости конденсатора по заряду и напряжению необходимо предварительно рассчитать его электрическое поле, исходя из общих соотношений для электрического поля.
Связь между зарядом и вектором смещения 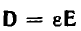
справедливой для линейных и нелинейных сред и являющейся основным соотношением для электрического поля. В правой части этого равенства стоит суммарный заряд, заключенный внутри замкнутой поверхности, в левой — поток вектора смещения. Смещение измеряется в к/м2, напряженность электрического поля — в в/м, диэлектрическая проницаемость в ф/м.
Поле в каждой точке характеризуется потенциалом 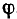
Напряжение 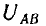
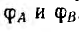
Потенциал также измеряется в вольтах.
Так как сумма напряжений по замкнутому пути равна нулю, то 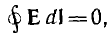
Емкость коаксиального кабеля
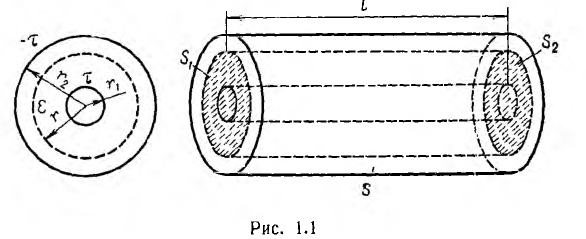
Коаксиальный кабель представляет собой два проводящих соосных
цилиндра с радиусом внутреннего цилиндра r1 внутренним радиусом
внешнего цилиндра г2, длиной цилиндров I (рис. 1.1).
Пусть внутренний цилиндр — жила кабеля — заряжен положительно и изолирован диэлектриком с проницаемостью е от оболочки — обратного провода, являющегося внешним цилиндром и несущим заряд обратного знака, а напряжение между жилой и оболочкой равно U.
При выполнении условия 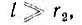
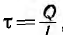
Для цилиндрической поверхности радиуса г, охватывающей заряженную жилу (на рис. 1.1 указана пунктиром), можно применить теорему Гаусса. Из- за радиального направления вектора смещения потоки через основания цилиндра 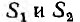
Так как при неизменном радиусе смещение D остается постоянным, то
В последние выражения не входит радиус 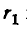
Напряжение на кабеле
откуда емкость кабеля
После подстановки из предпоследнего равенства
в выражение для напряженности поля получим
т .е . напряженность поля обратно пропорциональна радиусу, а ее максимальное значение у поверхности жилы
Исследование на минимум показывает, что наименьшее значение
максимальной напряженности при заданных напряжении и радиусе 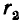
внешней оболочки будет при
т. е. при 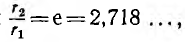
При таком соотношении радиусов кабель, очевидно, обладает наибольшей электрической прочностью.
Емкость двухпроводной линии
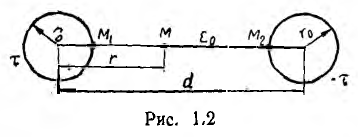
Широко используемые в электротехнике двухпроводные линии передачи представляют собой систему двух прямых параллельных проводов кругового сечения (рис. 1.2). Провода оказываются заряженными разноименно, когда линия включена на напряжение.
Так как длина проводов I велика по сравнению с расстоянием d между их осями, искажением электрического поля у концов заряженных проводов можно пренебречь. Поэтому распределение поля в пространстве остается неизменным в любой плоскости, перпендикулярной осям проводов.
Пусть двухпроводная линия подвешена настолько высоко, что влиянием земли можно пренебречь. Напряжение на линии равно U, величина заряда на единицу длины — τ, радиус проводов — 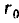
В отличие от коаксиального кабеля, где вследствие равномерного распределения заряда по поверхности жилы ее электрическая ось совпадает с геометрической, плотность зарядов на проводах линии больше на частях их поверхностей, обращенных друг к другу из-за притяжения разноименных зарядов. Поэтому расстояние между электрическими осями проводов становится тем меньше расстояния между их геометрическими осями, чем меньше отношение 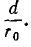
Для воздушных линий 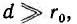
где 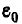
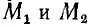
Отсюда емкость двухпроводной воздушной линии
Взаимоёмкость и ее расчёт
Для многих технических задач представляет интерес рассмотрение электрического поля, созданного системой нескольких пар разноименно заряженных тел. Заряды этих тел и напряжения связаны между собой линейными уравнениями.
В системе из двух конденсаторов (1-1′ и 2-2′ на рис. 1.3) все четыре тела связаны электрическим полем, поэтому заряд каждого из конденсаторов зависит от их напряжений 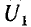
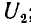
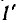
напряжением второго, совпадает по знаку с зарядом, создаваемым собственным напряжением, суммарные заряды обоих конденсаторов будут:
где 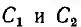
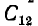
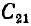
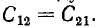
Собственные емкости конденсаторов
определяются всеми четырьмя телами системы и отличаются от емкости каждого из этих конденсаторов, определенной при отсутствии другого.
При определении ёмкости 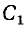
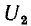
Соответственно, при определении 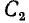
т. е. равна отношению заряда на обкладках накоротко замкнутого одного конденсатора, когда его заряд создается напряжением другого, к этому напряжению.
Взаимоемкость определяется конфигурацией тел, образующих конденсаторы, их взаимным расположением и пропорциональна диэлектрической проницаемости среды.
При несовпадении знаков собственных зарядов, обусловленных емкостью, и взаимных зарядов, обусловленных взаимоемкостью, знак перед вторыми членами в выражениях (1.2) будет отрицательным. Взаимоемкость также измеряется в фарадах (ф).
Для системы многих конденсаторов, соответственно, заряд Qk
конденсатора k определяется всеми напряжениями:
где 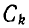
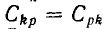
Взаимоемкость между конденсаторами k и р равна отношению заряда конденсатора k, созданного напряжением конденсатора р, к этому напряжению. При этом все конденсаторы, кроме p -того, замкнуты накоротко.
Взаимоемкость двух параллельных двухпроводных линий
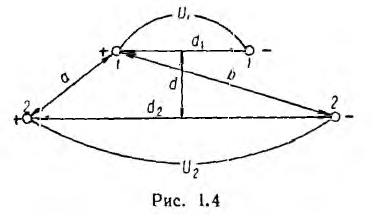
Примером системы из четырех тел, рассматриваемой как совокупность двух конденсаторов, могут служить две параллельные линии, расположенные симметрично одна над другой (рис. 1.4).
Пусть радиус проводов 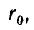
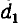
и 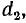

Заряды на проводах первой линии замкнутой накоротко 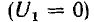
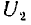
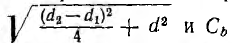
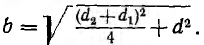
Тогда, соответственно формуле (1.1), получается
а собственная емкость первой линии при учете второй линии равна
Такая задача представляет технический интерес, позволяя определить влияние линии передачи 2 на линию связи 1 (рис. 1.4).
Это влияние состоит в наведении на проводах линии связи заряда взаимоемкости 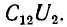
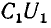
а напряжение 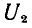
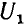
линии связи, то для уменьшения наведенного заряда необходимо увеличивать расстояние d между линиями и уменьшать расстояние 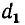
между проводами линии связи.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линейные н нелинейные диэлектрики и конденсаторы
- Сопротивление и его расчет
- Линейные и нелинейные резисторы
- Индуктивность и ее расчет
- Преобразование схем электрических цепей
- Установившиеся процессы в линейных электрических цепях
- Методы расчета простых электрических цепей
- Метод сигнальных графов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник