Магнитная индукция коаксиального кабеля формула

Индуктивность коаксиального кабеля

Коаксиальный кабель представляет собой два длинных соосных прово­дящих цилиндра, пространство между которыми заполнено каким-либо изолирующим материалом с магнитной проницаемостью m. Пусть а — радиус внутреннего цилиндра, а b — внешнего. Длина кабеля обычно во много раз превышает его радиус. Поэтому магнитное поле, создава­емое электрическим током в кабеле, будет таким же как у бесконечно длинного кабеля, если не учитывать искажения поля у его концов.

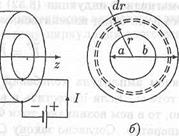
Найдем индуктивность участка кабеля длиной l. Для этого создадим замкнутую электрическую цепь из внутреннего и внешнего цилиндров кабеля и подключим к этой цепи источник постоянной ЭДС (рис. 8.6, а).Токи, создаваемые этой ЭДС, потекут по поверхностям цилиндров вдоль их оси в противоположных направлениях.

В силу цилиндрической симметрии системы силовые линии магнит­ного поля суть семейство окружностей, центры которых лежат на оси симметрии. На рис. 8.6, а изображена одна из силовых линий. Для определения напряженности магнитного поля применим теорему (7.7) о циркуляции вектора Н . В качестве контура интегрирования С выберем силовую линию произвольного радиуса г. Циркуляция вектора напря­женности по такому контуру буд

Hdl= H dl =H dl = Н 2pr. (8.33)

Рис. 8.6. Коаксиальный кабель

Если радиус контура С меньше радиуса внутреннего цилиндра (г 6), сумма токов равна нулю, так как токи в цилиндрах имеют противоположные направления. Поэтому напряженность магнитного поля Я = 0 при г Ь, т.е. магнитное поле внутри малого цилиндра и вне большого отсутствует. Если радиус контура С таков, что а 2 = (1/2) m I 2 /8p 2 r 2 . (8.35)

Найдем энергию магнитного поля внутри кабеля. Для этого рассмо­трим цилиндрический слой, образованный двумя воображаемыми цилин­драми радиусов r и r + dr (рис. 8.6, б).Если длина слоя равна l, то его объем dV = 2prldr. Так как плотность энергии (8.35) зависит только от г, внутри тонкого цилиндрического слоя она будет всюду одна и та же. Поэтому энергия магнитного поля в слое

Проинтегрировав это выражение по r в пределах от а до b, найдем энер­гию магнитного поля на участке кабеля длиной l:

W = (1/4p) m I 2 l =(1/4p) m I 2 l ln(b/a) (8.36)

С другой стороны, энергию магнитного поля можно определить по формуле (8.26). Приравняем эти выражения и найдем индуктивность участка коаксиального кабеля длиной l:

Взаимная индукция

Рассмотрим два контура с токами I₁ и I₂ (рис. 8.7), расположенные на некотором расстоянии друг от друга. Ток в первом контуре созда­ет магнитное поле, поток yкоторого через второй контур, очевидно, пропорционален силе тока I₂

Аналогично, магнитный поток Ф₁ через первый контур поля, создавае­мого током во втором контуре, пропорционален силе тока I₂.

Коэффициенты пропорциональности L₁₂ и L₂₁ называются взаимной ин­дуктивностью, или коэффициентами взаимной индукции. Они зависят от формы, размеров, взаимного расположения контуров и от магнитной проницаемости среды, в которой находятся контуры.

Рис. 8.7. Взаимная индукция

Рассмотрим простой пример. Пусть на одном цилиндрическом каркасе имеется две обмотки, образующие два соленоида одинаковой длины l(рис. 8.8). Число витков одного соленоида равно N₁, а второго — N₂. Найдем коэффициенты L₁₂ и L₂₁ для этой системы.

Рис. 8.8. К вычислению коэффициента взаимной индукции

редположим, что в первом соленоиде течет ток I₁, а во втором — 1₂. В силу (7.17) напряженность магнитного поля тока h внутри соленоида

Поток магнитной индукции этого поля через один из витков 2 соленоида

Так как поле внутри соленоида однородно, потоки через все витки оди­наковы. Поэтому потокосцепление

Аналогично, напряженность поля, создаваемого током I₂, будет

Поток магнитной индукции этого поля через один из витков первого соленоида

Отсюда найдем, что

Это равенство справедливо для двух любых контуров и составляет со­держание теоремы взаимности.

Вычислим энергию магнитного поля двух соосных соленоидов. Векто­ры напряженности полей, создаваемых токами I₁ и I₂, внутри соленоидов коллинеарны. Если токи I₁ и I₂ текут в одном направлении, то векто­ры H₁ и Н₂ сонаправлены. В этом случае суммарное магнитное поле характеризуется напряженностью:

Если же токи I₁ и I₂ текут в разных направлениях, то векторы Н₁ и H₂ направлены противоположно друг другу. При этом модуль напряженно­сти магнитного поля

Энергию однородного магнитного поля найдем по формуле (8.28):

При помощи формул (8.22) и (8.40), запишем это выражение так:

где первое слагаемое есть энергия тока в первом соленоиде, второе -энергия тока во втором, а третье слагаемое называется взаимной энерги­ей. Формула (8.42) справедлива в общем случае для двух произвольных контуров.

Задача. Найти взаимную индуктивность тороидальной катушки и проходящего по ее оси бесконечного прямого провода. Катушка имеет прямоугольное сечение. Внутренний радиус тороида равен а, внешний —b, а его высота — h. Число витков в катушке — N. Магнитная проницае­мость окружающей среды — m.

Источник

Индуктивность коаксиального кабеля.

Этим термином называют коэффициент, определяющий пропорциональное отношение между суммарным магнитным потоком (Фс) и электрическим током (I) в определенном контуре. Индуктивность проводника (L) и отмеченные параметры соединены в следующей формуле: Фc = I * L. Данная публикация поможет разобраться с тематическими вычислениями и применением теоретических знаний для расчета катушек, других специальных изделий.

Воздушные катушки индуктивности с различными рабочими характеристиками

Обозначение и единицы измерения

Упомянутый выше суммарный магнитный поток (Фс) также называется «потокосцеплением». Этот параметр определяет свойство определенного проводника препятствовать изменениям проходящего через него электрического тока. С его помощью можно найти величину созданной электродвижущей силы (Е), определить мощность (W):

Из приведенных выражений видно, что индуктивность проводника зависит от силы тока, который за определенное значение времени способен образовать ЭДС в замкнутом контуре.

К сведению. Следует учитывать тот факт, что при рассмотрении высокочастотного диапазона влияние индуктивности значительно даже при работе с прямыми участками проводников.

В стандартной международной системе единиц «СИ» данный параметр указывают в генри (Гн). 1 Гн соответствует контуру, который формирует в контрольных точках разность потенциалов 1V. Сила тока в катушке за одну секунду изменяется на 1 А.

Индуктивность коаксиального кабеля.

Коаксиальным кабелем называют систему, состоящую из прямолинейного цилиндрического проводника и охватывающей его, как правило, тонкостенной проводящей трубки кольцевого поперечного сечения. Электрический ток течет по внутреннему проводнику в заданном направлении. Точно такой же по величине электрический ток течет по внешнему проводнику в обратном направлении. Ниже рассмотрим конструкцию коаксиального кабеля, в которой внутренний проводник является тонкостенной цилиндрической оболочкой (рис. 1). Это предположение позволит нам не уточнять реальное распределение тока по внутреннему проводнику. Индуктивность коаксиального кабеля рассчитывается на единицу длины кабеля. Контур, на который натянута поверхность, пронизываемая силовыми линиями магнитного поля, охватывает плоскую радиальную поверхность между проводниками протяженностью в одну единицу длины.

С помощью теоремы о циркуляции вектора магнитной индукции убеждаемся в том, что магнитное поле внутри первой цилиндрической оболочки и вне второй цилиндрической оболочки равно нулю. Магнитное поле между цилиндрическими оболочками описывается выражением

Здесь и — радиусы внутренней и внешней оболочек соответственно, — текущий радиус, — сила тока, текущего по одному из проводников. Вектор магнитной индукции, величина которого определена соотношением (1), перпендикулярен описанной выше базовой плоской поверхности. Рассчитаем величину магнитного потока через эту поверхность:

Здесь волной над символом обозначена величина в пересчёте на единицу длины вдоль оси симметрии системы проводников. В соответствии с определением индуктивности находим индуктивность единицы длины коаксиального кабеля:

С помощью именно этой физической величины описываются квазистационарные электромагнитные явления в протяженных коаксиальных кабелях (например, уравнения телеграфистов, рассмотренные в одном из следующих разделов курса).

.
Индуктивность двухпроводной линии.
Рассмотрим два прямолинейных достаточно тонких проводника круглого поперечного сечения радиуса , расположенных в пространстве параллельно друг другу так, что расстояние между осями их поперечных сечений равно , при этом выполнено условие (рис. 1). Пусть по левому проводнику ток течёт «от нас», а по правому проводнику тот же ток течёт «к нам». В силу оговоренного выше условия распределение тока по поперечным сечениям проводников можно считать равномерным. Индуктивность двухпроводной линии рассчитывается на единицу длины. Магнитный поток при этом пронизывает поверхность единичной длины, эта поверхность опирается на контур, показанный на рис. 1.

Начало оси абсцисс расположим посередине между проводниками. Координата при этом изменяется от значения –(h/2-a) до значения (h/2-a).

Величина магнитной индукции от левого проводника описывается выражением: (1)

а от правого проводника в той же точке пространства – выражением (2)

Заметим, что векторы магнитной индукции и параллельны друг другу и одинаково направлены для всех точек плоскости, проходящей через рассматриваемые проводники, если эти точки лежат между проводниками. В этом случае величина результирующего магнитного поля в рассматриваемой области изменения переменной является суммой величин и . Вычислим результирующий магнитный поток через описанную выше поверхность:

Из соотношения (3) следует зависимость для погонной индуктивности двухпроводной линии при условии h>>a:

Зависимость (4) оказывается эффективным параметром двухпроводной длинной линии, рассчитанная с её помощью величина скорости распространения электромагнитной волны вдоль двухпроводной линии совпадает с величиной скорости волны, измеренной экспериментально.

Дата добавления: 2017-09-01; просмотров: 7501; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Узнать еще:

Теоретическое обоснование

Рассматриваемое явление основано на способности генерации магнитного поля проводником при пропускании через соответствующий контур электрического тока. Для облегчения расчетов возможны следующие допущения:

• слабость (медленное изменение) электрических полей;
• постоянная сила тока в каждой части контура;
• отсутствие емкостных составляющих проводника.

Резонанс в электрической цепи

Для элементарно малых областей эксперимента берут точечное распределение токов (магнитных полей). Суммирование расчетных параметров позволяет уточнить зависимость векторного представления индукции (B) от потока, пронизывающего поверхность S. Ее край формирует контур, по которому пропускают ток.

Чтобы не усложнять вычисления, рассматривают суммарный поток, проходящий через S, без учета сложности определенной поверхности. Он будет примерно равен току. Уточняющий коэффициент (L) помогает узнать действительное значение.

К сведению. На основе приведенных рассуждений можно сделать промежуточный вывод о минимальном значении формы контура (при работе с низкими и средними частотами).

Свойства индуктивности

Следующие особенности индуктивности (L) надо учитывать в ходе подготовки конструкторской документации:

• L > 0;
• L зависит от размеров рабочего контура;
• на L оказывают влияние магнитные свойства окружающей среды.

Значение индуктивности зависит от магнитных параметров материала сердечника

Индуктивность одновиткового контура и индуктивность катушки

По приведенным выше формулам несложно сделать расчет базовых параметров для одного витка. Общее значение Фс (потокосцепление) равно сумме потоков через каждый из контуров, при одинаковых размерах рабочих элементов Ln = L1 * N2, где N – количество витков.

Важно! В реальных условиях структура магнитных полей значительно отличается в центральной части и на краях катушки.

Индуктивность соленоида

Этим термином называют катушку с длиной, намного большей, по сравнению с диаметром. Такое соотношение геометрических размеров формирует параллельные силовые линии в центре конструкции. Для этой части индукция определяется по формуле:

В = m * N*I, где m (магнитная постоянная) = 4*π*10-7 Гн.

Индуктивность определяют с помощью выражения:

где:

• S – площадь поперечного сечения катушки;
• l – длина конструкции.

При установке внутрь сердечника с ферромагнитными свойствами дополнительно применяют поправочный множитель (m1), который определяет влияние соответствующего материала.

Индуктивность тороидальной катушки (катушки с кольцевым сердечником)

Для расчета изделий такой формы допустимо применять стандартную формулу со следующими поправками:

где r – радиус до центральной оси тора.

Индуктивность длинного прямого проводника

Такую конструкцию рассчитывают по формуле:

где mc (mi) – относительные проницаемости среды (материала проводника), соответственно.

При отсутствии внешних помех коэффициент mc берут равным единице.

ИНДУКТИВНОСТЬ

ОСНОВЫ ЭЛЕКТРИЧЕСКОГО РАСЧЕТА КАБЕЛЕЙ И ПРОВОДОВ Индуктивность цепи характеризуется отношением магнитного по­тока Ф к току I

, создавшему этот поток:

Индуктивность кабелей.измеряют и нормируют в генри, милли­генри (10–3 гн)

и микрогенри (10–6
гн)
на 1
км
или 1
м.
Индуктивность одножильного кабеля, а также внешняя индук­тивность коаксиального кабеля

Индуктивность коаксиального кабеля

Общая индуктивность коаксиального кабеля с медными внутрен­ним и внешним проводниками

В случае многопроволочного внутреннего проводника его диаметр

Индуктивность внутреннего проводника спирального радиоча­стотного кабеля задержки, выполненного в виде спирали поверх сер­дечника с магнитной проницаемостью μ c,

Индуктивность двухжильного неэкранированного кабеля (рис. 2-4)

Индуктивность двухжильного экранированного кабеля (рис. 2-5)

Индуктивность двухжильного кабеля с учетом магнитного пото­ка внутри жил:

где Q (x) — коэффициент, зависящий от коэффициента вихревых токов,

и радиуса жилы (табл. 2-2). С возрастанием частоты передаваемого тока общая индуктивность цепи уменьшается, а внешняя индуктивность не зависит от частоты.

Индуктивность двухпроводной линии (рис. 2-4), когда μ =1,

Индуктивность одиночного провода

При больших сечениях жил, а также при высоких частотах про­исходит уплотнение тока у периферии жилы, благодаря чему снижа­ется напряженность магнитного поля внутри жилы. С учетом этого на практике для определения индуктивности одиночного провода пользуются формулой

Индуктивность каждой жилы трехжильного кабеля или трех одножильных кабелей, расположенных по вершинам равносторонне­го треугольника, определяют аналогично (рис. 2–4,6). В случае трехжильного кабеля с секторными жилами за r

принимают радиус эквивалентной по сечению круглой жилы, а за
а
— расстояние меж­ду серединами малых хорд секторов в поперечном сечении кабеля.

В случае расположения трех одножильных кабелей в одной пло­скости (рис. 2–4,в

) индуктивность среднего кабеля определяют по приведенной выше формуле, но за
а
здесь принимают расстояние между осями двух соседних кабелей. Индуктивность крайних ка­белей

и
i
с — сила тока в крайних проводах А и С.

Приведенные формулы подсчета индуктивности справедливы в случае небронированных кабелей. При наличии в непосредственной близости к кабелю магнитных материалов (например, проволочная или ленточная броня) индуктивность таких кабелей соответственно возрастает, в этом случае

— магнитная проницаемость брони кабеля;
D
2— диаметр ка­беля поверх брони,
мм;D1
— диаметр кабеля под броней,
мм.
В трехжильном кабеле в каждый момент времени сумма вели­чин тока в трех жилах равна нулю и результирующий магнитный поток в пространстве, окружающем жилы, в некотором удалении от них практически также равен нулю; поэтому в трехжильных кабелях влиянием магнитной брони на индуктивность пренебрегают.

Индуктивное сопротивление жилы кабеля

Индуктивность искусственной цепи в четверке

а в четверке типа двойной пары (ДП)
← Предыдущая | Следующая → … содержание …

Таблица индуктивностей

Закон полного тока

Катушка индуктивности в цепи переменного тока проявляет себя различным образом. По мере увеличения частоты большее влияние начинает оказывать так называемый «скин» эффект. Его вызывают поверхностные токи. Для коррекции распределения полей применяют поправочные множители. В некоторых ситуациях приходится дополнительно учитывать воздействие вихревых составляющих.

Таблица с формулами для расчета самоиндукции типовых замкнутых контуров

Датчики

Поперечное сечение проводника

Изменение напряжения на катушке индуктивности используют для контроля параметров окружающей среды. Такие датчики чутко реагируют на приближение изделий с ферромагнитными свойствами. Их применяют для бесконтактной фиксации положения отдельных частей механизмов, створок ворот и других изделий.

В соответствующем исполнении они хорошо противостоят неблагоприятным внешним воздействиям. Потенциальных потребителей привлекают простота, разумная стоимость, долговечность. Функциональный датчик несложно сделать собственными руками при необходимости. Такие приборы без проблем совмещаются с другими компонентами систем автоматизации.

Источник