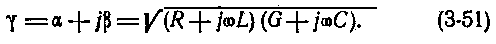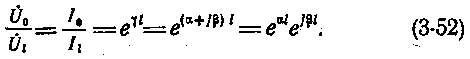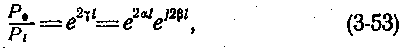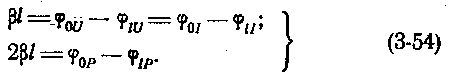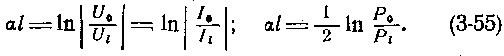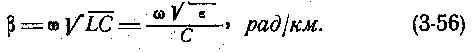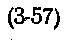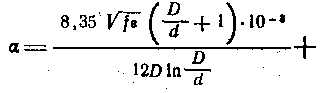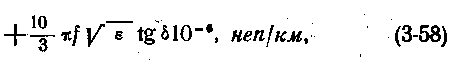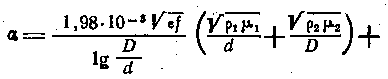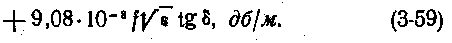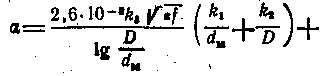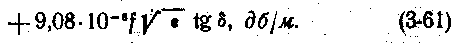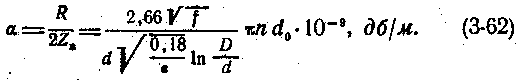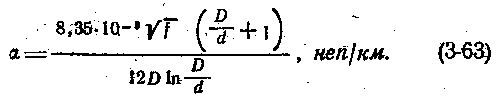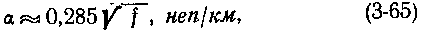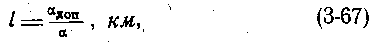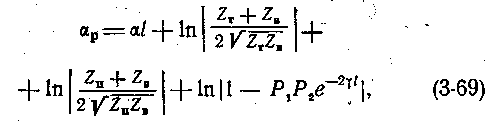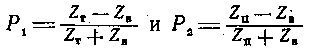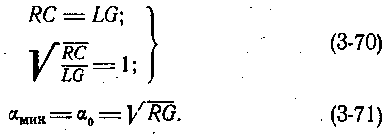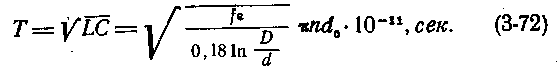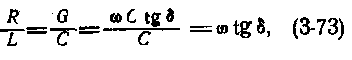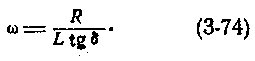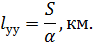Коэффициент распространения, затухания и фазы кабеля
Электромагнитная энергия, распространяясь вдоль кабеля, уменьшается по величине от начала к концу линии. Уменьшение или затухание энергии происходит вследствие потерь на нагревание жил и поляризацию молекул изоляции. С ростом частоты потери увеличиваются. Потери в изоляции учитываются посредством коэффициента распространения γ, являющегося комплексной величиной:
Приведенные выше уравнения для тока и напряжения можно представить в следующем виде:
Модуль этого выражения (е αt ) характеризует уменьшение абсолютного значения тока или напряжения при прохождении по линии длиной l. Аналогичны выражения для затухания мощности:
где α — коэффициент затухания (затухание на длине 1 км).
Угол φ = βl , характеризующий изменение угла вектора тока или напряжения на участке линии длиной l, называется коэффициентом фазы или фазовой постоянной:
Таким образом, коэффициент распространения одновременно определяет изменение сигнала как по абсолютной величине, так и по фазе на 1 км длины кабеля. Логарифмируя обе части уравнений (3-54), получаем формулы для расчета величины затухания:
Затухание принято измерять в неперах (неп) на 1 км. Затухание 1 неп — затухание кабельной цепи, у которой ток или напряжение в начале ее больше по абсолютной величине, чем ток или напряжение в конце, в 2,718 раза (е=2,718), т. е. αl = 1. В радиочастотных кабелях затухание обычно выражают в децибелах (дб) на 1 м (1 неп=8,65 дб; 1 дб = 0,115 неп).
Фазовая постоянная (коэффициент фазы)
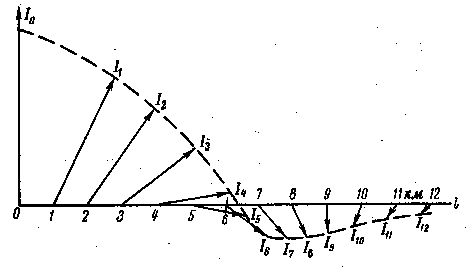
Рис. 3-8. Изменение тока вдоль однородной линии.
Фазовая постоянная измеряется в радианах на 1 км или градусах (1 рад = 57,3°).
Фазовая постоянная измеряется в радианах на 1 км или градусах (1 рад = 57,3°).
На рис. 3-8 приведена кривая изменения тока вдоль однородной линии. В табл. 3-1 приведены сокращенные формулы для подсчета α и β в различных диапазонах частот.
Затухание коаксиального радиочастотного кабеля
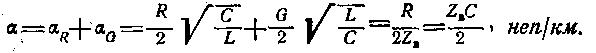
Подставив в (3-57) значения R, L,C и G, получим:
или после преобразований
Если внутренний и внешний проводники кабеля изготовлены из медной проволоки, то
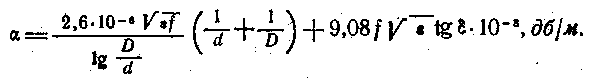
При многопроволочном внутреннем проводнике и оплетке — внешнем проводнике
Затухание спиральных радиочастотных кабелей (кабелей задержки)
Затухание коаксиальных кабелей связи
При оптимальном геометрическом отношении диаметров внешнего и внутреннего проводников D/d=3,6
Затухание коаксиального кабеля с полиэтиленовой шайбовой изоляцией
где f — частота, Мгц.
Затухание симметричного радиочастотного кабеля
На рис. 3-9 приведена зависимость затухания α и фазовой постоянной β от частоты. Дальность связи по кабельной линии
где α — коэффициент затухания кабеля, неп/км; α доп — допустимое затухание кабельной линии, неп.
По существующим нормам затухание линий низкочастотной телефонной связи (НЧ) должно быть не более 3,3 неп, а высокочастотных линий (ВЧ) — 6 — 7 неп.
Предельно допустимая дальность связи по магистральным кабельным линиям
где τ — допустимое время прохождения сигнала, мксек; по нормам Международного консультативного комитета время прохождения сигналов от одного абонента к другому не должно превышать 250 мксек, а для кабельных линий, соединенных с международными магистралями, 100 мксек; Т — время пробега сигнала на участке линии длиной 1 км, мксек/км.
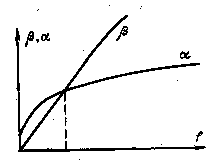
Рис. 3-9. Зависимость коэффициента затухания а и коэффициента фазы Р от частоты.
В неоднородных линиях затухание складывается из собственного затухания кабеля и затухания из-за неоднородности электрических характеристик. Дальность связи по такой кабельной линии будет обусловливаться ее рабочим затуханием α р , являющимся затуханием кабельной линии в рабочих условиях (при любых нагрузочных сопротивлениях на концах). Кроме собственного затухания кабеля αl, рабочее затухание учитывает также несогласованность на соединениях кабелей с нагрузками Z T и Z n . Рабочее затухание определяется по формуле
— коэффициенты отражения на стыках генератор — кабель и приемник — кабель. Первое слагаемое в правой части этого уравнения — собственное затухание кабеля, второе и третье — дополнительные затухания вследствие несогласованности сопротивлений генератора и кабеля (Z r ≠ Z B ), приемника и кабеля (Z n ≠ Z B ), четвертое — дополнительное затухание вследствие взаимодействия нёсогласованностей в начале и конце линии.
Затухание линии имеет минимальное значение при следующих соотношениях первичных параметров:
На рис. 3 — 10 приведены изменения коэффициентов затухания в токопроводящих жилах α ж и в изоляции α и при различных значениях 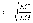
Таким образом, затухание кабеля может быть снижено путем уменьшения R, т. е. увеличения диаметра внутреннего проводника (токопроводящих жил) и соответствующего увеличения расхода меди; затем путем уменьшения G, т. е. применения изоляционных материалов с более высокими электроизоляционными свойствами, затем уменьшения С, т. е. увеличения толщины изоляции и соответственно увеличения расхода материалов, наконец, искусственного увеличения L.
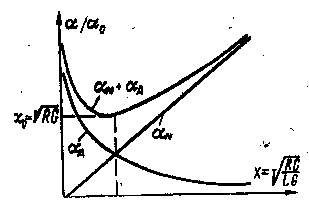
Рис. 3-10. Затухание в жилах и изоляции кабеля при различных соотношениях первичных параметров кабеля.
Известно несколько различных способов искусственного увеличения индуктивности кабельных линий: пупинизация (включение в кабель катушек индуктивности через определенные расстояния), крарупизация (нанесение на токопроводящую жилу проволоки или ленты из сплава с большой магнитной проницаемостью), биметаллизация (нанесение на токопроводящую жилу электролитическим путем слоя железа) и применение магнитодиэлектрика поверх токопроводящей жилы (например, полиэтилена, наполненного ферритом или альсифером). Практическое применение в кабельной технике получил способ пупинизации в низкочастотных кабелях связи, а способ искусственного увеличения индуктивности путем применения магнитодиэлектрика используют в спиральных радиочастотных кабелях (кабелях задержки) и помехозащищенных автомобильных проводах высокого напряжения.
В результате возникновения продольного магнитного поля, направленного вдоль оси спирального коаксиального кабеля, резко возрастает общее магнитное поле кабеля и соответственно увеличивается индуктивность его. Время распространения сигналов в таком кабеле
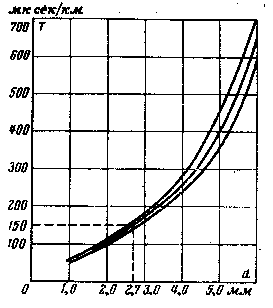
Рис. 3-11. Зависимость времени распространения сигналов Т от диаметра кабеля.
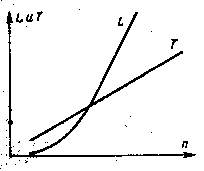
Рис. 3-12. Зависимость изменения времени распространения сигналов Т и индуктивности L от числа витков спирального кабеля.
На рис. 3-11 приведена зависимость времени распространения сигналов Т от диаметра кабеля. С увеличением диаметра спирального кабеля время распространения сигналов возрастает. На рис. 3-12 приведена зависимость времени распространения сигналов Т и индуктивности L от числа витков спирального кабеля. Возрастание индуктивности спирального кабеля находится в квадратичной зависимости от увеличения числа витков. Емкость и проводимость изоляции спиральных кабелей незначительно выше, чем у обычных коаксиальных радиочастотных кабелей. Активное сопротивление и затухание существенно возрастают с увеличением числа витков п, уменьшением диаметра эмалированного провода для изготовления спирального проводника кабеля и возрастанием частоты. По этой причине практическая максимальная частота спиральных кабелей не превышает 30 Мгц. С возрастанием частоты соотношение RC = LG в кабеле нарушается. Объясняется это увеличением проводимости изоляции с возрастанием частоты. Это условие выполняется только при определенной частоте (без искусственного повышения индуктивности):
Для симметричных кабелей связи частота f ж = ω х /2π находится в пределах 200-600 кгц.
Источник
Расчет проводимости изоляции симметричного кабеля
Согласно [1, формула 5.69], уравнение для расчета проводимости симметричного кабеля имеет вид:
С – емкость кабеля (рассчитано выше), Ф/км;
ω = 2πf – циклическая частота, Гц;
tg δ – тангенс угла диэлектрических потерь согласно, [2, таблица 3]);
G0 – проводимость, обусловленная токами утечки, из за несовершенности материала. Так как современные изолирующие материалы достаточно качественны, то данное значение стремиться к нулю. В расчетах данным слагаемым пренебрегаем.
Подставим значения и произведем вычисления для f1 = 12 кГц:
Расчеты для других частот проведем по аналогичной методикой табличным способом. Промежуточные и конечные результаты представим в таблице 1.
Расчет вторичных параметров:
5. Расчет коэффициента затухания симметричного кабеля:
Согласно [1, таблица 4.6], уравнение для расчета коэффициента затухания симметричного кабеля имеет вид:
R – километрическое сопротивление симметричного кабеля (рассчитано выше), Ом/мм 2 ·км;
L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;
С – емкость симметричного кабеля (рассчитано выше), Ф/км;
G — проводимость симметричного кабеля (рассчитано выше), Ф/км.
Подставим значения и произведем вычисления для f1 = 12 кГц:
Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 1.
6. Расчет коэффициента фазы симметричного кабеля:
Согласно [1, таблица 4.6], уравнение для расчета коэффициента фазы симметричного кабеля имеет вид:
ω = 2πf – циклическая частота, Гц;
L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;
С – емкость симметричного кабеля (рассчитано выше), Ф/км;
Подставим значения и произведем вычисления для f1 = 12 кГц:
Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 1.
7. Расчет волнового сопротивления симметричного кабеля:
Согласно [1, таблица 4.6], уравнение для расчета волнового сопротивления имметричного кабеля имеет вид:
L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;
С – емкость симметричного кабеля (рассчитано выше), Ф/км;
Подставим значения и произведем вычисления для f1 = 12 кГц:
Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 1.
Так как волновое сопротивления не зависит от частоты, то данное значение верно на всех заданных частотах.
8. Расчет фазовой скорости волны симметричного кабеля:
Согласно [1, таблица 4.6], уравнение для расчета скорости распространения волны в симметричном кабеле имеет вид:
L – километрическая индуктивность симметричного кабеля (рассчитано выше), Гн/км;
С – емкость симметричного кабеля (рассчитано выше), Ф/км;
Подставим значения и произведем вычисления для f1 = 12 кГц:
Так как волновое сопротивления не зависит от частоты, то данное значение верно на всех заданных частотах.
Сведем все рассчитанные значения в итоговую таблицу 1 и построим графики.
Таблица 1 – Рассчитанные значения первичных и вторичных параметров передачи от различных значениях частоты в заданном диапазоне
| Параметр | Частота f, кГц | |||
| Первичные параметры симметричного кабеля | ||||
| R, Ом/км | 119,699 | 164,424 | 219,585 | 291,239 |
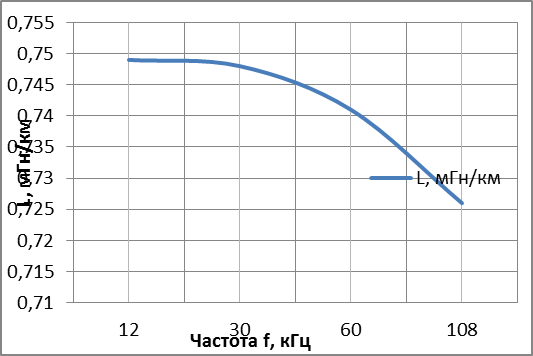
| L, мГн/км | 0,749 | 0,748 | 0,741 | 0,726 |
| С, нФ/км | 21,333 | 21,333 | 21,333 | 21,333 |
| G, мкСм/км | 0,723 | 2,813 | 8,038 | 21,704 |
| Вторичные параметры симметричного кабеля | ||||
| a, дБ/км | 0,3194 | 0,4392 | 0,589 | 0,790 |
| b, рад/км | 0,301 | 0,7531 | 1,499 | 2,672 |
| Zв, Ом | 187,402 | 187,27 | 186,436 | 184,57 |
| Vф, км/с | 250,124 | 250,291 | 251,42 | 253,94 |
По рассчитанным значениям первичных и вторичных параметров симметричного кабеля, построим графики зависимостей коэффициентов передачи от частоты. Графики представлены на рисунках 1 и 2.
 |  |
 |  |
| Рисунок 1 – Частотные зависимости первичных параметров симметричного кабеля | |
 |  |
 |  |
| Рисунок 2 – Частотные зависимости вторичных параметров симметричного кабеля |
Задача 2
Рассчитать защищенность между цепями симметричного кабеля на длине усилительного участка в заданном диапазоне частот и построить частотную зависимость данного параметра влияния.
Построить графики частотной зависимости защищенности на дальнем конце в заданном диапазоне частот. По результатам расчетов сделайте сравнение с нормами и дайте заключение о пригодности кабеля с данными симметричными цепями для заданной системы связи.
| Параметр | S, дБ | К, пф/сд | Заданный диапазон, кГц | Частоты, кГц |
| f1 | f2 | f3 | f4 | |
| Значение | 12-108 |

Согласно [1, формулы 6,27; 6,28; 6,29] для симметричного кабеля характерины справедливы уравнения.
Переходное затухание на ближнем конце:
Переходное затухание на дальнем конце:
Защищенность симметричной линии:
l – длина участка регенерации, км;
a — кило метрическое затухание сигнала в кабеля (рассчитано в задаче 1);
N12 – электромагнитная связь на ближнем конце;
F12 – электромагнитная связь на дальнем конце;
N12, F12 упрощенно определяются согласно [1, стр. 264-265]:
Длину усилительного участка рассчитаем по приближенной формуле согласно [2, формула 3]:
a — коэффициент затухания цепи при частоте f (рассчитано 1 задачей);
S — энергетический потенциал аппаратуры.
Считаем, что оборудование ЦСП и следовательно S = 35 дБ.
Подставим значения и произведем вычисления для f1 = 12 кГц:
Переходное затухание на ближнем конце:
Переходное затухание на дальнем конце:
Защищенность симметричной линии:
Расчеты для других частот проведем по аналогичной методикой табличным способом. Конечные результаты представим в таблице 2.
Таблица 2 – Рассчитанные значения переходных затуханий на ближнем, дальнем конце и защищённость симметричной линии связи в заданном диапазоне частот
| Параметр | Частота, кГц | |||
| A0, дБ | 78,061 | 71,492 | 66,789 | 81,99 |
| Al, дБ | 111,6 | 105,0307 | 100,328 | 115,537 |
| Aз, дБ | 76,6 | 70,03 | 65,32 | 80,537 |
По рассчитанным значениям переходных затуханий и защищённости симметричного кабеля, построим графики зависимостей рассчитанных параметров от частоты. Графики представлены на рисунке 3.
Рисунок 3 – График зависимости переходных затуханий от частоты
Приведем нормы на переходные затухания А0 для симметричного кабеля и сравним рассчитанные параметры с нормативными приведенные в таблице 3 и сделаем вывод.
Таблица 3 – Нормативные и расчётные значение переходных затуханий
| Параметр | Норма на НЧ симметричную, четырехпров. линия Aз, дБ | Частота, кГц | ||
| Нормативное значение, дБ | 65,1+ al | 100,1 | ||
| Расчетное значение, дБ | 76,6 | 70,03 | 65,32 | 80,53 |
Проверка показала, что нет необходимости повышать параметры взаимного влияния между симметричными цепями, так как они находятся в пределах нормы.
Задача 3
Рассчитать параметры двухслойных стеклянных волокон оптического кабеля. Разработать конструкцию кабеля и нарисовать эскиз поперечного сечения в масштабе 10:1.
Расчету подлежат: числовая апертура NА; нормированная частота ν; число типов волн N, распространяющихся в кабеле; диаметр сердцевины волокна для одномодовой передачи d, мкм; коэффициент затухания волны в волокне кабеляa, дБ/км; уширение импульса в кабеле tи, мкс/км.
| Параметр | Диаметр сердцев 2а, мкм | Диаметр оболочки 2в, мкм | Потери в сердцевине tgd·10 — 11 | Длина волны l , мкм |
| Значение | 1,2 | 1,5 |
| Параметр | Коэффициент преломления сердцевины n1 | Коэффициент преломления оболочки n2 | Число волокон в кабеле, м | Длина регенерационного участка lр, км |
| Значение | 1,5 | 1,48 |
Определим основные оптические параметры стекловолокна с точность до 4 цифры после запятой, согласно методике приведенной в [4, стр. 145-146] и в методических указаниях [2, формулы 6-9].
NA – числовая апертура ОВ;
n1 и n2 — коэффициент преломления сердцевины и оболочки;
Значение апертурного угла:
Θa = arcsin(NA) = arcsin(0,244) = 4,13, рад.
Значение нормированной частоты:
Так как v > 2,405, то можно сделать вывод, что для данного типа ОВ имеет место многомодовый режим работы.
Число типов волн (мод) N, которые одновременно распространяются по оптическому волокну, рассчитывают по формуле:
Полученное значение округлять до меньшей целой величины.
Для того чтобы по оптическому волокну распространялась только волна НЕ11, диаметр сердцевины волокна должен выбираться из условия:
Затухание света в волокне оптического кабеля обусловлено поглощением энергии в материале стекловолокна, а также рассеянием в окружающее пространство. Приближенно суммарный коэффициент затухания вычислять по формуле:
Величину tи рассчитать по формуле согласно [1, стр. 209] для заданной длины регенерационного участка:
с = 3·10 5 км/с – скорость света в вакууме.
Приведем возможную конструкцию волоконно-оптического кабеля в разрезе, учитывая число волокон и укажем основные элементы конструкции.
Эскиз поперечного разреза кабеля приведен на рисунке 4.
Рисунок 4 – Поперечный разрез волоконно-оптического кабеля
Список литературы
1. Гроднев И.И., Верник С.М. Линии связи. – М.: Радио и связь, 1988 г. -354 с.
2. Комаров Ю.З., Направляющие системы электросвязи: Методические указания и контрольные задания по выполнению домашней контрольной работы. – Екатеринбург: УрТИСИ ГОУ ВПО «СибГУТИ», 2006. -19 с.
3. Иванов А.Б. Волоконная оптика: компоненты, системы передачи, измерения – М.: Компания Сайрус Системс, 1999. -672 с.
4. Горлов Н.И., Микиденко А.В., Минина Е.А., Оптические линии связи и пассивные компоненты ВОСП: Учебное пособие. Новосибирск; Сиб.ГУТИ — 2003 г. –245 с.
5. Андреев В.А., Бурдин В.А., Попов Б.В., Польников А.И., Строительство и техническая эксплуатация волоконно-оптических линий связи: Учебник для ВУЗов, М.: Радио и связь, — 1995, -220 стр.
Источник