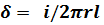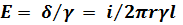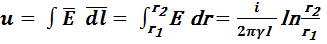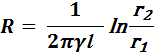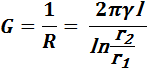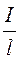Коаксиальный кабель ток утечки

Расчет сопротивления изоляции коаксиального кабеля

Вопрос о пространственном распределении тока важен, например, при исследовании токов в земле, токов в массивных проводниках, токов проводимости в изоляции.

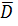
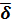
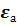
Между соотношениями, характеризующими стационарное электрическое поле постоянных токов и электростатическое поле в диэлектрике можно провести формальную аналогию. Формальное совпадение будет, если в уравнениях электростатического поля вектор заменить на вектор , а абсолютную диэлектрическую проницаемость кдельной проводимостью .

В электростатике граница диэлектрика это проводник и она яляется эквипотенциалью. Вектор 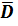будет нормален к этой границе проводника.

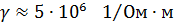
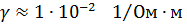
В проводящих средах существуют области с плохо проводящей средой (почва, несовершенная изоляция диэлектрика). Например, при выполнении заземлителей из стальных стержней удельная прповодимость стали , удельная прповодимость почвы .

В этом случае поверхность стали можно считать эквипотенциалью и вектор плотности тока в почве считать направленным ортогонально к стальному проводнику. На основании вышеизложенного можно утверждать, что картина электрического поля токов ( в почве или несовершенной изоляции) будет совпадать с картиной поля в соответствующих электростатических задачах.

В связи с этим можно ввести метод электростатической аналогии, позволяющий использовать результаты расчета электростатических задач для расчета соответствующих задач в проводящих средах.

Рассмотрим задачу расчета тока утечки коаксиального кабеля и сопротивления его несовершенной изоляции.

В сечении кабеля, изображенном на рисунке линии напряженности поля и линии тока утечки направленны радиально. Из принципа непрерывности тока получим

l – длина кабеля.

Напряжение между жилами кабеля

Сопротивление изоляции кабеля равно

а ее проводимость

Формулу для проводимости можно было написать сразу, пользуясь методом электростатической аналогии. Для этого достаточно в формуле для емкости кабеля

заменить 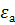на γ .

Дата добавления: 2020-03-21 ; просмотров: 680 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Электрическое поле в проводящих средах. Основные теоретические положения

Страницы работы

Фрагмент текста работы

Тогда ток утечки через изоляцию кабеля на длине в 1 км составит

Мощность тепловых потерь в изоляции Р = U∙I = 10000∙0,628 = 6280 Вт.

Задача 13.8. Однослойный коаксиальный кабель работает под напряжением 600 В и имеет размеры: r₁ = 4 мм, r₂ = 8 мм, l = 10 км, удельная проводимость изоляции g = 1∙10 -9 См/м. Определить ток утечки и его плотность в изоляции на поверхности жилы и на внутренней стороне оболочки кабеля, а также тепловые потери кабеля.

Задача 13.9. Рассчитать ток утечки между двумя жилами коаксиального кабеля (рис. 13.6). Изоляция выполнена двухслой-ной из несовершенного диэлектрика (удельные проводимости g₁ = 5·10 -8 См/м и g₂ = 2·10 -8 См/м, относительные диэлектриче-ские проницаемости e₁ = 2 и e₂ = 5). Напря-жение U = 10 кВ. Геометрические размеры – r₁ = 1 мм, r₂ = 2 мм, r₃ = 3 мм.

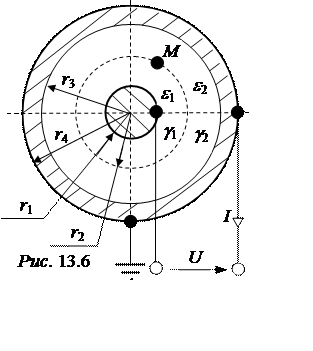
Найти удельные тепловые потери в окрестности точки М, проводимости и ёмкости между телами, построить схему замещения системы. Кабель считать весьма протяжённым, а расчеты выполнить на единицу длины.

Дополнительно определить предельно возможную длину кабеля как линии электропередачи.

1. Пусть ток утечки равен i. Тогда в соответствии с формулами (13.2) плотность тока, напряжённость и потенциал в слоях диэлектрика определяются по формулам

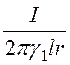
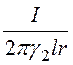
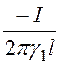
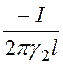
d = i/(2prl); Е₁ =, Е₂ =; j₁ =lnr+ А₁, j₂ =lnr + А₂.

2. Напряжение, приложенное к устройству,

=ln+ln=ln.

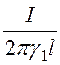
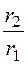
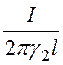
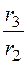
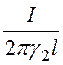
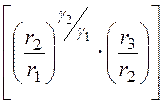
3. Отсюда ток утечки на единицу длины

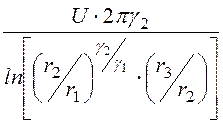
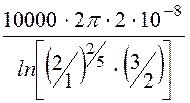
i₀ === 1,841·10 -3 А/м = 1,841 мА/м.

4. Проводимость кабеля токам утечки найдём по закону Ома:

5. Этот же ответ можно получить, используя аналогию между электрическим полем в проводящей среде и электростатическим. Формула ёмкости однослойного коаксиального кабеля (13.3): C₀ =.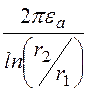

ёмкости слоёв и всего данного кабеля:

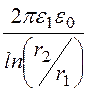
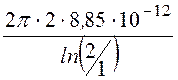
C₁₀ === 160,4 пФ/м;

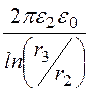
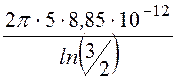
C₂₀ === 873,5 пФ/м;

так как ёмкости соединены последовательно, то

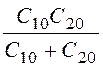
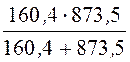
C₀ === 135,5 пФ/м.

Проводимости слоёв и всего кабеля на единицу длины:

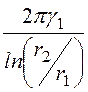
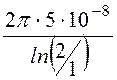
g₁₀ === 0,454·10 -6 Cм/м;

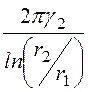
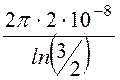
g₂₀ === 0,310·10 -6 Cм/м;

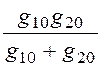
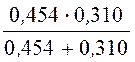
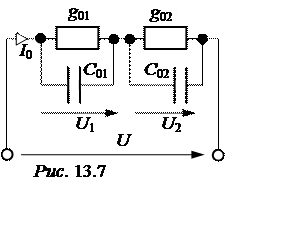
g₀ === 0,1842 мкСм/м.

6. Электрическая схема замещения устройства показана на рис. 13.7.

7. Плотность тока в окрестности точки М:

тепловые потери в окрестности точки М по закону Джоуля-Ленца:

8. Сечение внутренней жилы кабеля меньше, чем наружной, и рав-но S = pr₁ 2 = 3,14 мм 2 . Если принять, что жилы алюминиевые, а допустимая плотность тока 1 А/мм 2 , то допустимый ток для кабеля будет равен 3,14 А. Тогда допустимая длина кабеля (пока он ещё хоть сколько-нибудь способен питать нагрузку, а не целиком себя) –

А для получения приемлемого КПД эта длина должна быть ещё меньше.

Задача 13.10. Цилиндрический конденсатор с двухслойной изоляцией (рис. 13.6) работает при напряжении U = 10 кВ. Известны размеры конденсатора (r₁ = 0,08 см, r₂ = 0,2 см, r₃ = 0,6 см, l = 5 см) и свойства изоляции (g₁ = 1∙10 -8 См/см, e₁ = 2, g₂ = 4∙10 -8 См/см, e₂ = 6). Рассчитать ток утечки через изоляцию конденсатора, найти выражения удельной проводимости g₀ и ёмкости С₀ конденсатора.

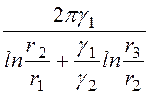
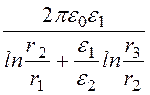
g₀ == 5,273∙10 -8 См/м, С₀ == 43,34 пФ/м.

Задача 13.11. Плоский конденсатор ёмкостью 10 мкФ находится под напряжением 1 кВ. Диэлектрическая проницаемость изоляции e = 4, а удель-ная проводимость g = 1∙10 -12 См/м. Определить ток утечки между обклад-ками конденсатора.

Задача 13.12. Два плоских конденсатора С₁ = 0,2 мкФ, С₂ = 0,5 мкФ с несовершенными диэлектриками соединены последовательно и подключа-ются к источнику напряжения U = 1200 В. Диэлектрические проницаемости диэлектриков: e₁ = 2,4, e₂ = 4; удельные проводимости: g₁ = 0,2∙10 -9 См/м, g₂ = 5∙10 —9 См/м. Определить напряжения на каждом из конденсаторов в момент включения, а также в установившемся режиме.

При решении задачи воспользуемся схемой замещения системы, представленной на рис. 13.7. В момент включения весь ток проходит по незаряженным конденсаторам в соответствии со вторым законом комму-тации. То есть через конденсаторы проходит один и тот же заряд

Источник

Расчет тока утечки между двумя жилами коаксиального кабеля

Задачи

Задача 1

При заданном векторе плотности тока

δ= 4x ×1_x + 3y ×1_y — 7z ×1_z , ( А/мм 2 )

определить значение потенциала φ (В) вида φ= Ax2 + By2 + Cz2 в точке с

координатами x=3 (м), y=2 (м), z=1 (м) при известной удельной проводимости среды γ=10·10 6 (1/Ом·м).

Решение. Переведем заданный вектор плотности тока δ в (А/м 2 ) и

по закону Ома в дифференциальной форме запишем вектор напряженности:

δ =0,4x 1x+ 0,3y 1y+ 0,7z 1z ,).

Далее на основании уравнения

В результате зависимость для потенциала будет следующей

тогда искомое значение потенциала в точке с координатами x=3 (м),y=2 (м), z=1 (м) составит:

j = -0,2 × (3)2 — 0,15× (2)2 + 0,35× (1)2 = -2,05 (В).

Задача 2.

Рассчитать ток утечки между двумя жилами коаксиального кабеля. Изоляция выполнена двухслойной из несовершенного диэлектрика (удельные проводимости g₁ = 5·10 -8 См/м и g₂ = 2·10 -8 См/м, относительные диэлектриче-ские проницаемости e_r1 = 2 и e_r2 = 5). Напряжение U = 10 кВ. Геометрические размеры – r₁ = 1 мм, r₂ = 2 мм, r₃ = 3 мм.

Найти удельные тепловые потери в окрестности точки М, проводимости и ёмкости между телами, построить схему замещения системы. Кабель считать весьма протяжённым, а расчеты выполнить на единицу длины.

Дополнительно определить предельно возможную длину кабеля как линии электропередачи.

Воспользуемся аналогией между электрическим полем в проводящей среде и электростатическим. ёмкости слоёв данного кабеля:

Проводимости слоёв и всего кабеля на единицу длины:

U2

U1

g02

C01

I0

U

g01

C02

Электрическая схема замещения устройства.

Плотность тока в окрестности точки М:

Удельные тепловые потери в окрестности точки М в слоях изоляции по закону Джоуля-Ленца :

p₁ = d 2 /g₁ = 0,147 2 /(5·10 -8 ) = 0,432·10 6 Вт/м 3 = 0,432 МВт/м 3 ;

p₂ = d 2 /g₂ = 0,147 2 /(2·10 -8 ) = 1,08·10 6 Вт/м 3 = 1,08 МВт/м 3 .

Задача 3. Заземлитель в виде шара

Заземлитель в виде шара расположен на сравнительно не­большой глубине h, соизмеримой с его радиусом R.

Применим к решению задачи метод зеркальных отображений. Заменим в верхней полуплоскости диэлектрик проводящей средой γ и зеркально расположим там такой же заземлитель, при этом граничные усло­вия на поверхности земли не из­менятся (линии вектора Е направлены по каса­тельной вдоль поверхности). Заменим токи, стекающие с поверхностей обоих заземлителей, равными по величине точечными токами, растекающимися из электрических центров 1 и 2, которые будут смещены относительно геометрических центров так, чтобы сохранились прежними граничные условия на по­верх­ности шаров (поверхности должны остаться эквипотенциальными с потен­циалом φ=U).

После определения положения электрических центров расчет па­раметров поля в произ­вольной точке n производится по методу наложения:

При соотношении h>>R потенциал на поверхности заземлителя будет ра­вен:

, откуда следует формула для определения сопротивления заземлителя:

Задача 4.

Определить шаговое напряжение на заданном расстоянии х от центра опоры высоковольтной ЛЭП при коротком замыкании одной из фаз линии на опору.

Для упрощения расчетов будем считать, что заземлитель опоры имеет форму полу­шара с радиусом R. Заменим диэлектрик в верхней части пространства проводящей средой γ, а заземлитель дополним зеркальным отображе­нием до полного шара. После таких преоб­разований решение задачи сводится к расчету поля шарового заземлителя:

где — фазное напряжение ЛЭП, R – радиус заземлителя (фундамента) опоры.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник