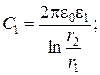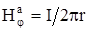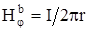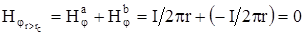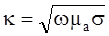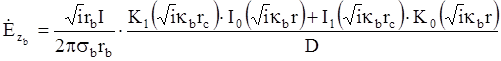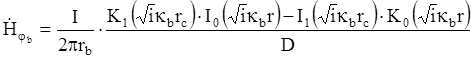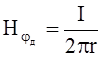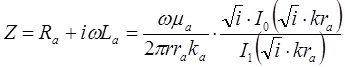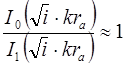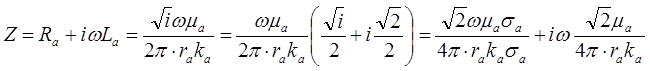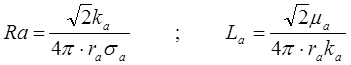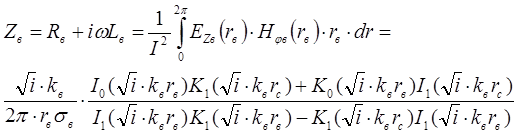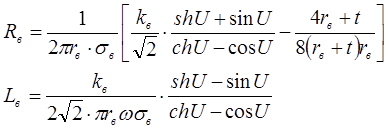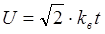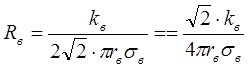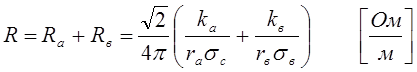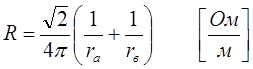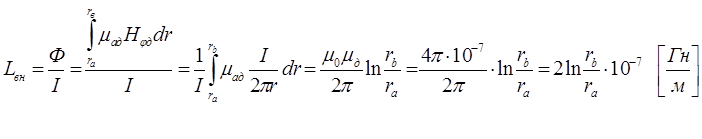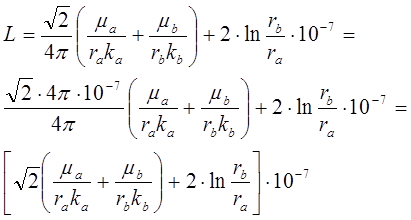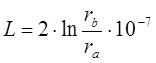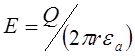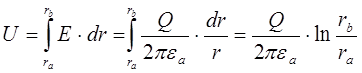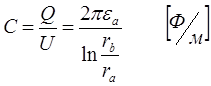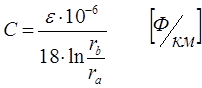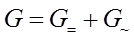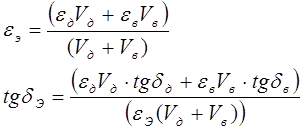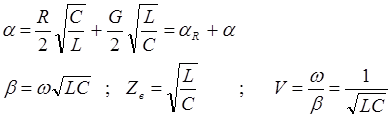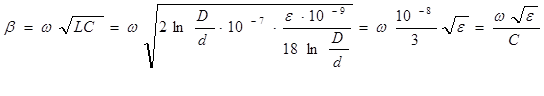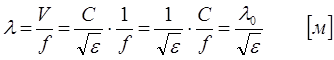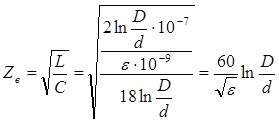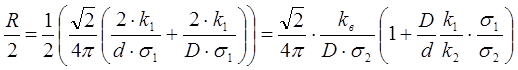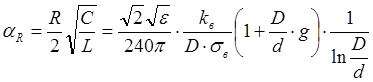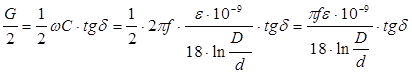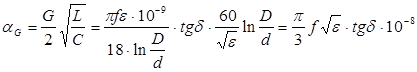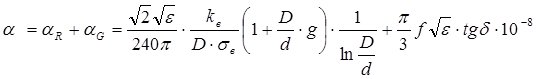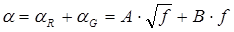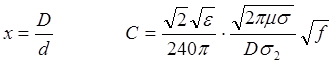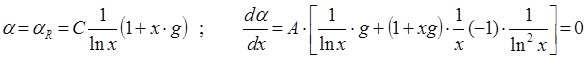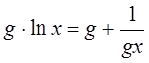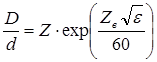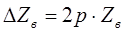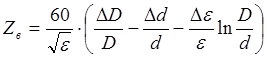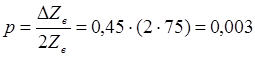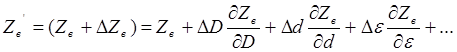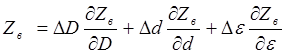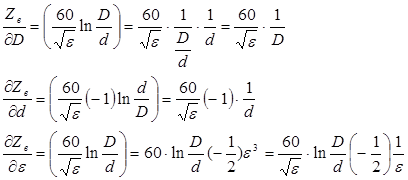Коаксиальный кабель напряженность поля

Коаксиальный кабель. Цилиндрический конденсатор

Коаксиальным кабелем называется система двух цилиндрических проводников различного радиуса, размещенных один внутри другого так, что их оси совпадают. Электрическое поле зарядов, расположенных на внутреннем проводнике, может быть заменено полем зарядов, расположенных на оси внутреннего проводника, как это делалось в случае заряженного проводящего шара. Поскольку обычно длина кабеля существенно больше его диаметра (диаметра наружного проводника), то для расчета параметров поля кабеля могут быть применены формулы (2.14), (2.15). Пусть потенциал наружного проводника равен нулю, тогда потенциал внутреннего проводника равен:

(2.16)

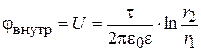
Емкость кабеля на единицу длины определяется как:

(2.17)

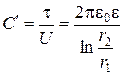
Напряженность поля в кабеле определяется выражением (2.14):

(2.18)

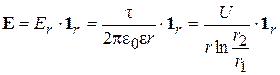
Цилиндрическим конденсатором называется система из двух электродов цилиндрической формы различного радиуса имеющих общую ось и вставленных один в другой. Любой отрезок коаксиального кабеля может рассматриваться как цилиндрический конденсатор. Если не учитывать влияния краев, то для расчета емкости и напряженности поля в цилиндрическом конденсаторе можно использовать формулы для коаксиального кабеля (2.16) – (2.18).

Как следует из формулы (2.18), наибольшая напряженность электрического поля в цилиндрическом конденсаторе будет при минимальном значении текущего радиуса r, которое равно r₁, т.е. напряженность максимальна на поверхности внутреннего электрода. Рассмотрим вопрос о нахождении оптимального размера внутреннего электрода, при котором напряженность на нем будет минимальна при заданных размерах внешнего электрода r₂ и потенциала U. Как следует из формулы (2.18), напряженность будет минимальна тогда, когда знаменатель в формуле будет максимален. Для нахождения экстремума этой функции нужно взять производную по r₁ и приравнять нулю:

,откуда . (2.19)

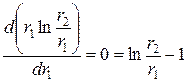
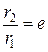
При заданном напряжении между обкладками цилиндрического конденсатора (коаксиального кабеля) наименьшая напряженность на внутренней обкладке (центральной жиле) будет при отношении радиусов равном основанию натуральных логарифмов е = 2,718281828459…

Коаксиальный кабель с двухслойным диэлектриком

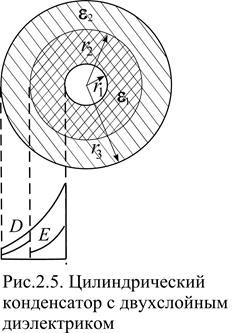
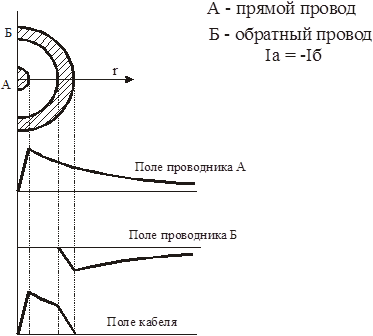
Для выравнивания напряженности электрического поля вдоль радиуса применяются многослойные диэлектрики с различными величинами диэлектрической проницаемости. На рис.2.5 показан коаксиальный кабель (цилиндрический конденсатор) с двухслойным диэлектриком и изменение электрического смещения и напряженности электрического поля вдоль радиуса кабеля. Радиус внутренней жилы, первого слоя диэлектрика, а также внешней оболочки, который совпадает с радиусом второго слоя диэлектрика, обозначены соответственно r₁, r₂ и r₃. Диэлектрические проницаемости первого и второго слоя диэлектрика обозначены e₁ и e₂. Пусть к обкладкам приложено напряжение U, а граница раздела диэлектриков совпадает с одной из эквипотенциальных поверхностей. В соответствии с теоремой о единственности картина поля не изменится, если разместить на границе раздела диэлектриков тонкую металлическую обкладку. Двухслойный конденсатор в этом случае может быть рассмотрен как два однослойных цилиндрических конденсатора вложенных один в другой, т.е. соединенных последовательно. В этом случае их емкость можно рассчитать по формуле емкости двух последовательно соединенных конденсаторов С₁ и С₂:

; (2.20)

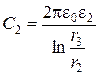
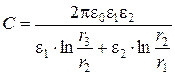
Напряженность поля может быть определена следующим образом: из равенства линейной плотности зарядов t = С×U = С₁×U₁ = С₂×U₂; получаем U₁= С×U/C₁, U₂= С×U/C₂ и напряженности в первом и втором слое диэлектрика:

(2.21)

. (2.22)

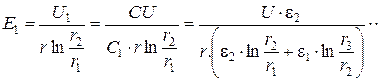
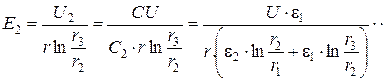
На границе раздела диэлектриков напряженность (радиальная составляющая) испытывает скачок, как это и следовало ожидать в соответствии с выражениями (1.40)-(1.42). В то же время величина вектора электрического смещения D₁=e₁E₁= D₂=e₂E₂ непрерывна. На рис. 2.5 приведены зависимости напряженности и электрического смещения в зависимости от радиуса для случая, когда e₁ > e₂. При таком выборе диэлектриков удается добиться выравнивания напряженности вдоль радиуса и существенно снизить напряженность вблизи центральной жилы.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Электрические процессы в коаксиальных кабелях связи

Коаксиальные кабели относятся к закрытым направляющим системам.

Закрытыми–называются направляющие системы поля, которых не выходят за пределы геометрических размеров этой системы.

По сравнению с другими кабелями коаксиальные кабели наи­более полно отвечают требованиям высокочастотной связи и между­городного телевизионного вещания. По коаксиальному кабелю можно передавать очень широкий спектр частот при сравнительно малых потерях энергии; кабель этот хорошо защищен от влияния соседних цепей и внешних помех, и также система связи в целом бо­лее экономична.

В металлической толще проводника магнитное поле возрас­тает, а вне его оно уменьшается по закону:

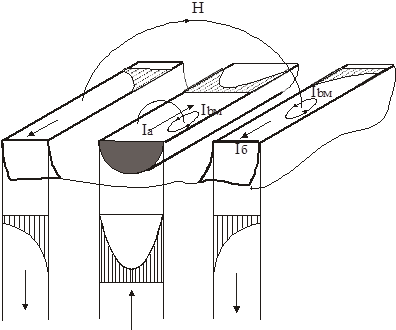
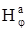
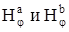
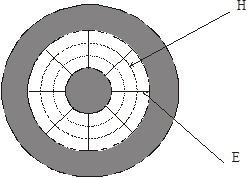
Внутри полого цилин­дра магнитное поле отсутствует, а вне его оно выражается таким же уравнением, как и для сплошного проводника:

Токи в проводниках а и b равны по значению и противоположны по знаку, поэтому маг­нитные поля внутреннего и внешнего проводников в любой точке пространства вне кабеля также равны по значению и направлены в противоположные стороны, следовательно результирующее магнит­ное поле вне кабеля равно:

Таким образом, линии магнитной ин­дукции поля коаксиального кабеля располагаются в виде концен­трических окружностей внутри него. Вне кабеля магнитное поле от­сутствует.

Электрическое поле также замыкается внутри коаксиального кабеля по радиальным направлениям между проводниками а и b, и поэтому вне кабеля это поле равно нулю. В коаксиальном кабеле из-за отсутствия внешнего поля потерь в окружающих его металличе­ских массах нет, все энергия распространяется только внутри кабеля и более эффективно передается к цепи.

Ø Рассмотрим действие поверхностного эффекта и эффекта бли­зости в коаксиальных кабелях и определим характер распределения плотности токов в проводниках при различных частотах.

Распределение плотности тока в проводнике, а определяется действием поверхностного эффекта. Перераспределение плотности тока по сечению проводника обусловлено эффектом близости к нему другого проводника.

На рис.3 показано переменное магнитное поле, создаваемое током проводника а, которое наводит в самом провод­нике а и в металлической толще полого проводника b вихревые токи , влияние которых приводит к перераспределению плотности тока по сечению проводников. Токи в проводниках а и b коаксиальной цепи как бы смещаются и концентрируются на взаимно–обращенных поверхностях проводников. Чем выше частота тока, тем сильнее эффект смещения тока на внешнюю поверхность проводника а и внутреннюю поверхность проводника b. Энергия как бы вытесня­ется из металлической толщи проводников и сосредотачивается внутри коаксиального кабеля, в изоляции, а проводники задают лишь направление распространения волн электромагнитной энергии.

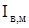
Мешающее электромагнитное поле высокой частоты, созда­ваемой соседними цепями передачи или другими источниками по­мех, действуя на внутренний проводник коаксиальной пары, также будет распространяться не по всему сечению кабеля, а лишь по его наружной поверхности. Таким образом, внешний проводник коакси­альной пары выполняет две функции:

1) является обратным провод­ником цепи передачи;

2) защищает (экранирует) передачу, веду­щуюся по кабелю от мешающих влияний.

Из рис. 4 видно, что основной ток передачи концентрируется на внутренней поверхности внешнего проводника, а ток помех–на на­ружной стороне внешнего проводника. Как основной ток, так и ток помех проникают в толщу проводника лишь на глубину, опреде­ляемую коэффициентом вихревых токов. Причем чем выше частота, тем больше отделяются друг от друга указанные токи и, следова­тельно, кабель лучше защищен от действия посторонних помех. Та­ким образом, в отличие от всех других топов кабелей, требующих для защиты от помех специальных мер в коаксиальных кабелях на высоких частотах это обеспечивается самой их конструкцией. Из из­ложенного следует, что основные преимущества коаксиального ка­беля (малое затухание и высокая помехозащищенность) особенно ярко проявляются в высокочастотном диапазоне. При низких часто­тах, когда ток практически проходит по всему сечению проводника, достоинства этого кабеля пропадают. Больше того, коаксиальная цепь как несимметричная относительно других цепей и земли (па­раметры ее проводников а и b различны) в низком диапазоне частот по защищенности от помех уступает симметричным кабелям.

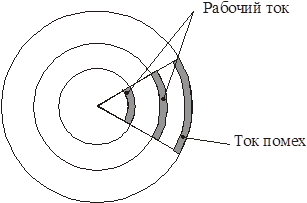
Электромагнитное поле коаксиальной цепи

Предположим, что ось кабеля совпадает с z. Тогда вследствие цилиндрической симметрии э/м поле не будет зависеть от коорди­наты j и все производные по j будут равны нулю. Кроме того, по физическим соображениям будет отсутствовать составляющая Н_z на­пряженности магнитного поля по оси z, тангенциальная составляю­щая напряженности электрического поля Е_j и радиальная состав­ляющая напряженности магнитного поля Н_r. Следовательно, для ко­аксиального кабеля останутся лишь составляющие э/м поля.

В результате э/м поле коаксиальной цепи определится следующими уравнениями:

(1)

(2)

(3)

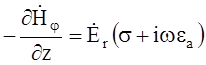
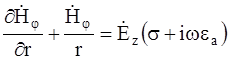
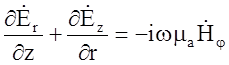
Эти уравнения полностью характеризуют э/м поле коаксиального кабеля идеальной конструкции, как в проводнике, так и в диэлектрике.

Найдем выражения для составляющих поля в отдельных эле­ментах коаксиального кабеля. В проводниках кабеля радиальная со­ставляющая напряженности электрического поля Е_r равна нулю. Кроме того, s>>iwe_a. При этих условиях уравнения (1)–(3) можно записать так:

(4)

(5)

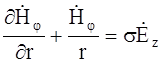
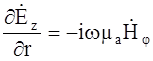
В результате получим волновое уравнение аналогичное сим­метричной цепи:

(6)

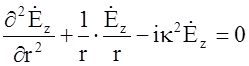
где

Решением является: 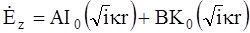(7)

Для внутреннего проводника напряженность электрического поля E_z, и напряженность магнитного поля Н_j опреде­ляются аналогично, как и для одиночного цилиндрического провод­ника (см. соответствующий раздел по симметрическим цепям).

(8)

(9)

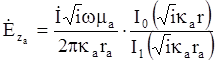
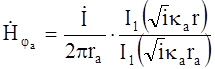
Для внешнего проводника напряженность электрического поля определяется уравнением (7). Напряженность магнитного поля определится:

(10)

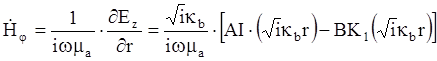
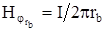
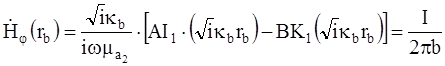
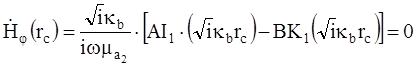
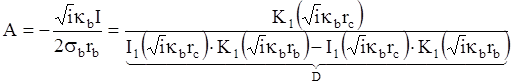
Для определения постоянных интегрирования, воспользуемся граничными условиями, согласно которым напря­женность магнитного поля на внутренней поверхности внешнего проводника по закону полного тока равна , а напряженность на его внешней поверхности равна нулю. Тогда:

(11)

(12)

(13)

Обозначим знаменатель через D:

(14)

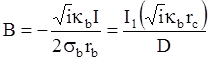
Подставим значе­ния А и В в формулы (7) и (10), получим следующее выражение для напряженности электрического и магнитного полей во внешнем проводнике:

Напряженность магнитного поля в пространстве между про­водниками коаксиального кабеля связана с электрическим током, протекающим по внутреннему проводнику кабеля, законом полного тока:

3.5.2 Определение сопротивления и индуктивности

Поскольку электромагнитное поле внешнего проводника никакого действия на внутренний проводник не оказывает, то полное сопротивление внут­реннего проводника определяется:

При больших 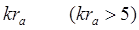соответст­вующем высокочастотной области передачи отношение

Тогда

Откуда

Для оп­ределения полного сопротивления внешнего проводника снова вос­пользуемся теоремой Умова–Пойтинга, согласно которой

По этой формуле можно рассчитывать R_В и L_В при любой частоте тока.

Для практических расчетов при 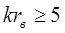(это выполняется для мед­ных проводников при частоте 60кГц и выше) сопротивление R и ин­дуктивность L может быть определены по формулам

где t = r_c-r_в ;

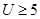
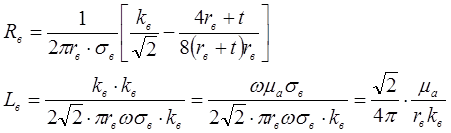Если вели­чина , то значение sinU и cosU в сравнении с shU » chU можно пренебречь. Тогда

Для частот свыше 60кГц в формуле для определения R вторым слагаемым в скобке по отношению к первому можно пре­небречь и тогда

Полное сопротивление прямого и обратного проводника определяется

Если внутренний и внешний провод­ник выполнен из одного материала, то

Полная индуктивность ко­аксиального кабеля определяется по формуле

L = L 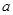+L_в+L_вн

Внешняя индук­тивность определяется как отношение магнитного потока Ф между проводником к току I, проходящему по коаксиальному кабелю

3.5.3 Определение емкости и проводимости коаксиальной цепи

При определении емкости коаксиального кабеля учитывают , что он аналогичен цилиндрическому конденсатору и его электриче­ское поле создается между двумя цилиндрическими поверхностями с общей осью. Напряженность электрического поля внутри кабеля на равнопотенциальной поверхности радиуса r определится как

Напряжение между внутренним и внешним проводниками

Тогда емкость коаксиального кабеля

Или при e_a = e₀e для 1 км получим

Изменить С можно только изменив e, т. к. используя комбинированную изоляцию

1) ПЭ порис­тый e = 1.4¸1.5;

где G₌ — проводимость постоянного тока;

— проводимость переменного тока;

Проводимость постоянного тока по отношению к проводимости переменного тока пренебрежительно мала, следовательно ;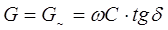

Где tgd — тан­генс угла диэлектрических потерь в изоляции.

Эквивалентные зна­чения коаксиальных кабелей с воздушно-комбинированной изоля­цией определяются по ранее приведенным формулам (для симмет­ричных кабелей)

3.5.4 Особенности расчета вторичных параметров

, где С = 3×10 8 м/c – скорость света.

называют коэффициентом укорочения, т.к.

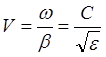
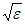
где l₀ – длина волны в вакууме.

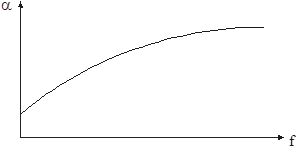
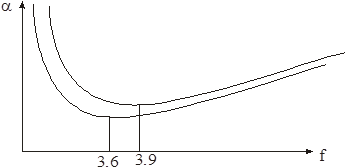
Зависимость a от частоты показана на рис.5.

Определим оптимальное соотношение .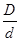

Пусть D = const, определим как изменяется a при изменении d .

Обозначим:

Откуда

Если , например , прямой и обратный провод выполнены из меди (g = 1 ), то оптимальное соотношение . Если прямой проводник выполнен из меди, а обратный из алюминия , тогда оптимальное соотношение .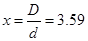

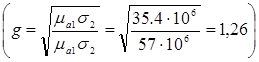
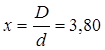
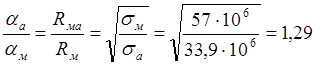
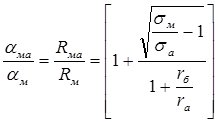
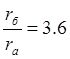
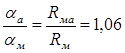
При замене медных проводников алюминиевыми затухание возрастает пропор­ционально соотношению активных сопротивлений или соответст­венно обратно пропорционально корню квадратному из проводимо­стей металлов , т.е. на 29 %. При замене только внешнего проводника на алюминиевый затухание возрастает в соотношении . При соотношении радиусов проводников получим , т.е. затухание возрастет лишь на 6 %.

Это дает основание сделать вывод о целесообразности применения коаксиальных кабелей с внешним алюминиевым про­водником. В этом случае затухание увеличивается всего на 6%, а расход меди на производство коаксиального кабеля сокращается на 65%. Потери в металле a_м изменяются пропорционально 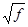, а по­тери в диэлектрике a_д связаны с частотой линейным знаком, и с уве­личением f возрастают значительно быстрее. В спектре частот уп­лотнение коаксиальных кабелей (до 8 МГц), используемом на прак­тике, в современных кабельных диэлектриках значение a_д незна­чительно и составляет 2-3% от a_м.

В кабелях со сплошной изоля­цией (e = 2,3 Z_в = 50 Ом), а в кабелях с комбинированной изоляцией » 75 Ом. Частотная зависимость волнового сопротивления в спектре от 60кГц и выше весьма незна­чительна, и волновое сопротивление можно считать постоянной ве­личиной.

Оптимальное соотношение диаметров проводников коаксиальной цепи

Конструирование коаксиальной пары подчинено задаче созда­ния оптимальной ее конструкции, требующей минимальных затрат материалов и средств на изготовление. При этом в первую очередь необходимо выбрать диаметры внутреннего и внешнего проводни­ков кабеля и установить наиболее выгодное из соотношений при ис­пользовании различных металлов (медь, алюминий, биметалл).

При конструировании коаксиального кабеля приходится также отступать от оптимального отношения D/d, если величина волно­вого сопротивления кабеля строго нормирования (например Z_{в =} 75 Ом). В этом случае отношение D/d определиться

Для получения норми­рованной величины Z_{в =} 75 Ом при оптимальном отношении D/d (a = min ) необходимо иметь воздушно-пластмассовую изоляцию с малым содержанием диэлектрика (e = 1.05), т.е. необходимо увеличивать D/d. При сплошной изоля­ции (e = 2,3) соотношение D/d, обеспечивающее (Z_{в =} 75 Ом) должно быть равно 6,6. Таким образом, для междугородных кабелей связи, по которым необходимо обеспечить наибольшую дальность связи при выборе конструкции исходят из условия оптимального по затуханию соот­ношения (D/d = 3.6) с учетом получения нормированной величины Z_{в =} 75 Ом.

Рис.7 Зависимость a от частоты в зависимости от материала внешнего проводника: Алюминий – верхний график Медь – нижний график

3.5.5 Конструктивные неоднородности в коаксиальных кабелях.

При изготовлении кабеля может возникнуть деформация в виде эксцентриситет в расположении проводников, нарушается и форма, постоянство взаимного расположения. В результате изменя­ются параметры кабеля, и он перестает быть однородным по длине.

Различают два вида неоднородностей: внутренние — в пределах строительной длины кабеля; стыковые, обусловленные различием характеристик соединяемых строительных длин. Стыковые неодно­родности, как правило, превышают внутренние.

Неоднородность кабеля сказывается главным образом на его волновом сопротивлении, которое на участках неоднородностей от­личается от номинального,

Неоднородности цепи учитываются через коэффициент отра­жения

,

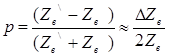
где 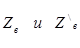— волновое сопротивление соседних неоднородных участков кабеля, отклонение волнового сопротивления.

Волновое сопротивление кабеля 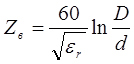и зависит от трех парамет­ров (e, d, D). Имея в виду, что неоднородность величин Dd, DD, De сравнительно не ве­лика, отклонение волнового сопротивления от среднего значения (волнистость) может быть выражено уравнением

Наибольшее влияние на колебания волнового сопротивления оказывают откло­нения размеров внешнего проводника и неоднородность изолирую­щих материалов, вызывающая колебания значений диэлектрической проницаемости. Внутренний проводник, представляющий сплош­ную проволоку, может быть изготовлен с большой точностью.

Для обеспечения требуемого качества связи и телевизионной передачи по коаксиальному кабелю необходимо, чтобы отклонение волнового сопротивления DZ_в, обусловленное отражениями внутри линии, не превышало 0,45 Ом, что соответствует коэффициенту от­ражения

С целью повышения однородности электрических ха­рактеристик коаксиальных магистралей производится специальное группирование строительных длин кабелей перед их прокладкой с таким расчетом, чтобы отклонения волнового сопротивления двух сменных строительных длин не превышали 0,3 Ом. При этом строи­тельные длины располагают так, чтобы волновые сопротивление по­степенно нарастали от начала усилительного участка к его середине и специалист середины к его концу.

Коаксиальные кабели бывают:

Отношение d/D	Число каналов
1 Микро коаксиальные В городских линиях	0.7/3.0	До 300
2 Малогабаритные Для зоновой связи (внутриобластной)	1,2/4,6	300, 1200
3 Среднегабаритные Для межзоновой связи	2,6/9,4	1920, 3600, 10800
4 Большие коаксиаль­ные Магистральная связь	7/27…11/40	До 50 000
5 Подводные Для повышения длины усилительного участка	5/18…8.4/25.4	До 720

Для определения влияния отклонений D и d на величину Z_в вос­пользуемся формулой разложения в ряд Тейлора, ограничиваясь лишь первыми членами ряда (для малых отклонений)

Дата добавления: 2017-01-16 ; просмотров: 6769 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник