ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ

Электрическое сопротивление токопроводящей жилы кабеля, провода и шнура постоянному току

где pv — удельное электрическое сопротивление, равное для алюминия 0,0263 ом-мм2/м, для меди 0,01752 ом* мм2м и для стали 0,139 ом*мм2/м.

Обычно сопротивление жил кабеля и провода пересчитывают на длину 1 км и сечение 1 мм2 и приводят к +20° С по формуле

где α — температурный коэффициент электрического сопротивления алюминия, равный 0,00403, меди ММ —0,00393 и МТ —0,00381 на 1°С при 20° С.

Сопротивление постоянному току биметаллического провода

где R01 и R02 — сопротивления первого и второго металлов.

Электрическое сопротивление любой жилы, скрученной в ка­бель, будет больше теоретического на величину укрутки א, равную 1,002—1,03 в зависимости от шага скрутки жилы кабеля, т. е.

Действующими ГОСТ предусмотрено, что электрическое сопро­тивление алюминиевых жил кабеля и провода не должно превы­шать 31,0 ом *мм2/км, а медных — 18,4 ом *мм2/км.

Активное сопротивление — это сопротивление, которое испыты­вает ток, проходя по цепи:

где R0 — сопротивление постоянному току; Rп.э— сопротивление по­верхностного эффекта; Rбл — сопротивление эффекта близости; Rм — сопротивление потерь в металле (в соседних жилах и в ме­таллической оболочке). На частоте до 10 кгц величина активного сопротивления считается практически неизменной, равной величине электрического сопротивления жил постоянному току Rо (рис. 2-1).

Отношение активного сопротивления жилы кабеля при переменном токе к сопротивлению при постоянном токе (Rf/R0) в зависимости от величины, пропорциональной квадрату параметра

приведено на рис. 2–2 (μ a = 4*10–9 гн/см — магнитная проницаемость алю­миния и меди; γ = 38*104 1/Ом*см — удельная проводимость меди).

Увеличение отношения активного сопротивления медных скру­ченных жил за счет поверхностного эффекта и эффекта близости при

переменном токе частотой 50 Щ к сопротивлению при постоянном токе Rf/R0 в зависимости от сечения жил силового кабеля приведе­но на рис. 2–3.

Активное сопротивление коаксиального кабеля

Коэффициент вихревых токов и глубины проникновения тока для различных металлов в зависимости от частоты приведены в табл. 2–1.

Активное сопротивление внутреннего проводника радиочастотно­го кабеля (многопроволочная конструкция) и внешнего проводника в виде оплетки

где k1 — коэффициент, учитывающий форму внутреннего проводника (отношение сопротивления многопроволочного проводника к сопротивлению эквивалентной сплошной конструкции проводника); прак­тически k для проводника 7 X0,26 мм равен 1 Г22, а для 7 X0,71 мм— 1,13; k2 — коэффициент, учитывающий форму внешнего проводника (отношение сопротивления внешнего проводника, выполненного в ви­де оплетки, к сопротивлению эквивалентной цилиндрической трубки). Коэффициент к2 зависит от конструкции оллетки: при диаметре ка­беля то изоляции до 4 мм равен 2; при диаметре от 4 до 6 мм — 2,5; от 6 до 7 мм — 3,0; от 7 до 8 мм — 3,5; свыше 8 мм — 4. Для внешнего проводника в виде обмотки прямоугольными проволока­ми к2 принимают равным 1,07—’1,1; dM = dn/2— диаметр эквивалент­ной многопроволочной жилы.

Активное сопротивление внутреннего и внешнего проводника из меди

Активное сопротивление внешнего проводника в виде лент, на­ложенных обмоткой под углом а, равно:

Активное сопротивление внутреннего проводника спирального радиочастотного кабеля задержки, выполненного в виде опирали из проволоки поверх сердечника диаметром d (см),

где d0 — диаметр между центрами проволоки спиральной обмотки, см; п — число витков на 1 м.

Активное сопротивление неэкранированных симметричных радио­частотных кабелей с расстоянием а между осями жил

кабеля с медными жилами

кабелей с медными многопроволочными жилами

Активное сопротивление цепи симметричных кабелей связи с уче­том поверхностного эффекта и эффекта близости (без учета потерь в окружающих металлических средах):

где 2 Rо — сопротивление цепи (из двух жил) постоянному току, ом/см; F(x) — коэффициент, учитывающий сопротивление, эквива­лентное потерям на вихревые токи, возбуждаемые внутренним маг­нитным полем (табл. 2-2); G(x)—коэффициент, учитывающий со­противление, эквивалентное потерям на вихревые токи, возбуждае­мые во второй жиле за счет эффекта близости |(табл. 2-2); Н (х) — коэффициент, учитывающий сопротивление, эквивалентное потерям на вихревые токи, возбуждаемые вторичным магнитным полем в пер вой жиле за счет эффекта близости (табл. 2-2); x=7,09

Коэффициент вихревых токов и глубины проникновения тока в зависимости от частоты

Дополнительное сопротивление (Rм), эквивалентное потерям в токопроводящих жилах смежных четверок и в свинцовой о5 олочке кабеля (f=200 кгц)

в кабелях с алюминиевыми жилами

;

с медными жи­лами

f — частота, гц; kc — коэффициент, учитываю­щий тип скрутки; парной скрутки (П) равный 1, четверки (Ч) — 5, двойной пары (ДП) — 1,73 и двойной четверки (ДЧ) —3.

Дополнительные сопротивления, эквивалентные потерям в со­седних четверках и в свинцовой оболочке,

где R200 — дополнительное сопротивление при частоте 200 кгц (табл. 2-3).

После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.

Источник

Электрическое сопротивление проводников

Понятие об электрическом сопротивлении и проводимости

Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.

Электронная теория так объясняет сущность электрического сопротивления металлических проводников. Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии.

Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.

Точно тем же объясняется сопротивление жидких проводников и газов прохождению электрического тока. Однако не следует забывать, что в этих веществах не электроны, а заряженные частицы молекул встречают сопротивление при своем движении.

Сопротивление обозначается латинскими буквами R или r .

За единицу электрического сопротивления принят ом.

Ом есть сопротивление столба ртути высотой 106,3 см с поперечным сечением 1 мм 2 при температуре 0° С.

Если, например, электрическое сопротивление проводника составляет 4 ом, то записывается это так: R = 4 ом или r = 4 ом.

Для измерения сопротивлений большой величины принята единица, называемая мегомом.

Один мегом равен одному миллиону ом.

Чем больше сопротивление проводника, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем легче электрическому току пройти через этот проводник.

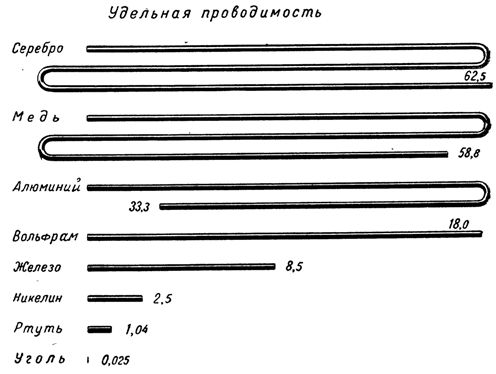
Следовательно, для характеристики проводника (с точки зрения прохождения через него электрического тока) можно рассматривать не только его сопротивление, но и величину, обратную сопротивлению и называемую, проводимостью.

Электрической проводимостью называется способность материала пропускать через себя электрический ток.

Так как проводимость есть величина, обратная сопротивлению, то и выражается она как 1/ R ,обозначается проводимость латинской буквой g.

Влияние материала проводника, его размеров и окружающей температуры на величину электрического сопротивления

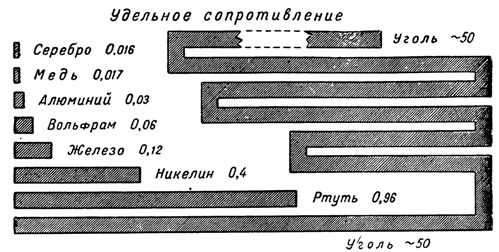
Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.

Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм 2 . Удельное сопротивление обозначается буквой греческого алфавита р. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.

Например, удельное сопротивление меди равно 0,017, т. е. медный проводник длиной 1 м и сечением 1 мм 2 обладает сопротивлением 0,017 ом. Удельное сопротивление алюминия равно 0,03, удельное сопротивление железа — 0,12, удельное сопротивление константана — 0,48, удельное сопротивление нихрома — 1-1,1.

Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.

Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.

Чтобы лучше понять эту зависимость, представьте себе две пары сообщающихся сосудов, причем у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая. Ясно, что при заполнении водой одного из сосудов (каждой пары) переход ее в другой сосуд по толстой трубке произойдет гораздо быстрее, чем по тонкой, т. е. толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т. е. первый оказывает ему меньшее сопротивление, чем второй.

Электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь площадь поперечного сечения проводника :

где — R — сопротивление проводника, ом, l — длина в проводника в м, S — площадь поперечного сечения проводника, мм 2 .

Площадь поперечного сечения круглого проводника вычисляется по формуле:

S = ( Пи х d 2 )/ 4

где Пи — постоянная величина, равная 3,14; d — диаметр проводника.

А так определяется длина проводника:

Эта формула дает возможность определить длину проводника, его сечение и удельное сопротивление, если известны остальные величины, входящие в формулу.

Если же необходимо определить площадь поперечного сечения проводника, то формулу приводят к следующему виду:

Преобразуя ту же формулу и решив равенство относительно р, найдем удельное сопротивление проводника:

Последней формулой приходится пользоваться в тех случаях, когда известны сопротивление и размеры проводника, а его материал неизвестен и к тому же трудно определим по внешнему виду. Для этого надо определить удельное сопротивление проводника и, пользуясь таблицей, найти материал, обладающий таким удельным сопротивлением.

Еще одной причиной, влияющей на сопротивление проводников, является температура .

Установлено, что с повышением температуры сопротивление металлических проводников возрастает, а с понижением уменьшается. Это увеличение или уменьшение сопротивления для проводников из чистых металлов почти одинаково и в среднем равно 0,4% на 1° C . Сопротивление жидких проводников и угля с увеличением температуры уменьшается.

Электронная теория строения вещества дает следующее объяснение увеличению сопротивления металлических проводников с повышением температуры.

При нагревании проводник получает тепловую энергию, которая неизбежно передается всем атомам вещества, в результате чего возрастает интенсивность их движения. Возросшее движение атомов создает большее сопротивление направленному движению свободных электронов, отчего и возрастает сопротивление проводника.

С понижением же температуры создаются лучшие условия для направленного движения электронов, и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов .

Сверхпроводимость , т. е. уменьшение сопротивления металлов до нуля, наступает при огромной отрицательной температуре — 273° C , называемой абсолютным нулем. При температуре абсолютного нуля атомы металла как бы застывают на месте, совершенно не препятствуя движению электронов.

Источник